はじめに

前回のLiNGAMの記事に引き続き、因果探索の手法に焦点を当てて、記事を書いていきたいと思い、ベイジアンネットワークについての記事を書くに至りました。正直なところ、ベイジアンネットワークについては、記事を書くまで、概念的な理解しかなく、どちらかというと初心者でした。ですが、最近話題になっているのもあり、今回記事を執筆するのを良い機会ととらえ、ベイジアンネットワークに関して頑張って学習した結果を記事に残したいと思います。最近因果推論に関する書籍は増えているものの、因果探索の書籍って少ないですよね...やはりPearl派の因果推論よりも、Rubin派の因果推論の方が、世間一般的に受け入れられているみたいな事情があるんですかね？
個人的には、Pearl派のバックドア基準をはじめとする考え方を、Rubin派の因果推論に持ち込むことによって、より実りのある因果推論につながると思っているので、前段として非常に有用な因果探索に関してももっと焦点が当たってもいいのになと思っています。また、論文を読めという話かもしれませんが、より高度なというか突っ込んだ話をしている書籍がこの先出てくれると、個人的にうれしいななんて思ってたりもします。まあこんな感じの愚痴はほどほどにしつつ、ベイジアンネットワークの内容に入っていこうと思います。

ベイジアンネットワーク

概要

ベイジアンネットワークは確率的グラフィカルモデルの一種で、変数間の確率的依存関係を表現する強力なツールです。この理論は、複雑なシステムにおける不確実性をモデル化し、推論を行うための基盤を提供します。

理論

ベイジアンネットワークは確率的グラフィカルモデルの一種で、変数間の確率的依存関係を表現する強力なツールです。この理論は、複雑なシステムにおける不確実性をモデル化し、推論を行うための基盤を提供します。ベイジアンネットワークの核心は、結合確率分布を条件付き確率の積として表現することにあります。 $n$ 個の変数 $X_1, X_2, ..., X_n$ からなるシステムを考えると、その結合確率分布 $P(X_1, X_2, ..., X_n)$ は以下のように分解できます

$P(X_1, X_2, ..., X_n) = \prod_{i=1}^n P(X_i | \text{Parents}(X_i))$

ここで、 $\text{Parents}(X_i)$ は変数 $X_i$ の親ノード（直接の原因）の集合を表します。この分解は、各変数がその親ノードにのみ直接依存するという仮定に基づいています。これにより、高次元の結合分布を、より扱いやすい低次元の条件付き分布の積として表現できるのです。

グラフ構造において、ノードは変数を、エッジは変数間の直接的な依存関係を表します。このグラフは有向非巡回グラフ（DAG）である必要があり、これにより因果関係の方向性を表現します。　　

ベイジアンネットワークの重要な概念の一つに、d分離（d-separation）があります。これは、グラフ上の任意の2つの変数集合が、第3の変数集合によって条件付き独立であるかどうかを判定する基準です。形式的には、変数集合 $X$ と $Y$ が変数集合 $Z$ によってd分離されているとき、以下が成り立ちます

$P(X | Y, Z) = P(X | Z)$

この条件付き独立性は、データから学習される確率分布と、グラフ構造から導かれる独立性の間の一貫性を保証する上で重要です。
　　
ベイジアンネットワークの学習は、構造学習とパラメータ学習の2段階に分けられます。構造学習では、データに最もフィットするグラフ構造を見つけることが目標となります。これには、スコアベースの手法や制約ベースの手法が用いられます。スコアベースの手法では、ベイズ情報量規準（BIC）などのスコアを最大化する構造を探索します

$\text{BIC} = \log P(D|\theta, G) - \frac{d}{2}\log N$

ここで、 $D$ はデータ、 $\theta$ はモデルパラメータ、 $G$ はグラフ構造、 $d$ はパラメータ数、 $N$ はサンプルサイズです。

　　
一方、パラメータ学習では、与えられたグラフ構造に対して、各条件付き確率分布のパラメータを推定します。最尤推定やベイズ推定などの手法が用いられ、例えば離散変数の場合、条件付き確率は以下のように推定されます

$P(X_i = x_i | \text{Parents}(X_i) = \pi_i) = \frac{N_{i,j,k}}{\sum_k N_{i,j,k}}$

ここで、 $N_{i,j,k}$ は、変数 $X_i$ が状態 $k$ をとり、その親が設定 $j$ である観測回数です。

ベイジアンネットワークの強力な機能の一つに、確率推論があります。これにより、一部の変数の観測値が与えられたときに、他の変数の確率分布を計算することができます。例えば、変数集合 $E$ の観測値 $e$ が与えられたときの変数 $X$ の事後確率は以下のように計算されます

$P(X|E=e) = \frac{P(X,E=e)}{\sum_X P(X,E=e)}$

この計算は、変数の数が多い場合に計算量が爆発的に増加する可能性があるため、ジャンクションツリーアルゴリズムなどの効率的な推論アルゴリズムが開発されています。
　　
一旦基本的なベイジアンネットワークの理論に関しては以上です。

モデル手順

データから可能な因果構造を推定します。この段階では、主に以下の二つのアプローチがあります

スコアベースの手法

可能な構造の空間を探索し、各構造にスコアを割り当てます。例えば、ベイズ情報量規準（BIC）を用いる場合

$\text{BIC} = \log P(D|\theta, G) - \frac{d}{2}\log N$

ここで、 $D$ はデータ、 $\theta$ はモデルパラメータ、 $G$ はグラフ構造、 $d$ はパラメータ数、 $N$ はサンプルサイズです。最高のスコアを持つ構造を選択します。

制約ベースの手法

条件付き独立性テストを繰り返し適用して、可能な因果構造を絞り込みます。例えば、PC algorithmでは、変数ペア $(X, Y)$ に対して

$P(X | Y, Z) = P(X | Z)$

を満たす変数集合 $Z$ を探します。この条件が成り立つ場合、 $X$ と $Y$ の間に直接の因果関係はないと判断します。

パラメータ学習

構造が決定したら、各ノードの条件付き確率分布のパラメータを推定します。離散変数の場合、最尤推定を用いると

$P(X_i = x_i | \text{Parents}(X_i) = \pi_i) = \frac{N_{i,j,k}}{\sum_k N_{i,j,k}}$

ここで、 $N_{i,j,k}$ は、変数 $X_i$ が状態 $k$ をとり、その親が設定 $j$ である観測回数です。

静的ベイジアンネットワーク実装

最も基本的なモデルは、静的なベイジアンネットワークです。これは、時間的な変化を考慮せず、変数間の瞬時的な関係のみを表現します。結合確率分布は以下のように表されます

$P(X_1, X_2, ..., X_n) = \prod_{i=1}^n P(X_i | \text{Parents}(X_i))$

このモデルは、比較的単純な因果関係の探索に適していますが、時間的な依存関係や複雑な相互作用を捉えることはできません。　　
今回使用する構造学習のアルゴリズムは、Hill-Climbing アルゴリズムです。Hill-Climbing アルゴリズムは、「丘を登る」という比喩に基づいているようです。現在の解から少しずつ改善を重ねることで、最適解（丘の頂上）に到達しようとします。Hill-Climbing アルゴリズムでは、ネットワーク構造の探索空間において、各構造にスコア（例：BIC、MDL、BDeu）を割り当て、そのスコアを最大化する構造を探索します。
アルゴリズムの手順は以下です。
初期構造（通常はランダム又は空のグラフ）現在の構造に対して、以下の操作を試みる
- エッジの追加 - エッジの削除 - エッジの反転
　　
これらの操作によって得られる新しい構造のスコアを計算します。
最も高いスコアを持つ構造が現在よりも良ければ、それを現在の構造とします。
改善が見られなくなるまで上記を繰り返します。
　　
実装は以下です（pgmpyを使用します）

import numpy as np
import pandas as pd
from pgmpy.models import BayesianNetwork
from pgmpy.estimators import BayesianEstimator, HillClimbSearch, BayesianEstimator
from pgmpy.inference import VariableElimination
import pydot

# より複雑なサンプルデータの生成
np.random.seed(42)
n_samples = 5000

# 変数A（根ノード）
A = np.random.binomial(n=1, p=0.6, size=n_samples)

# 変数B（Aに依存）
B = np.where(A == 1, 
             np.random.binomial(n=1, p=0.7, size=n_samples),
             np.random.binomial(n=1, p=0.3, size=n_samples))

# 変数C（AとBに依存）
C = np.where((A == 1) & (B == 1),
             np.random.binomial(n=1, p=0.9, size=n_samples),
             np.where((A == 1) | (B == 1),
                      np.random.binomial(n=1, p=0.5, size=n_samples),
                      np.random.binomial(n=1, p=0.1, size=n_samples)))

# 変数D（Bに依存）
D = np.where(B == 1,
             np.random.normal(loc=1, scale=0.5, size=n_samples),
             np.random.normal(loc=-1, scale=0.5, size=n_samples))

# 変数E（CとDに依存）
E = 2*C + 0.5*D + np.random.normal(loc=0, scale=0.1, size=n_samples)

# 変数F（DとEに依存）
F = np.where((D > 0) & (E > 1),
             np.random.exponential(scale=2, size=n_samples),
             np.random.exponential(scale=1, size=n_samples))

# データフレームの作成
data = pd.DataFrame({'A': A, 'B': B, 'C': C, 'D': D, 'E': E, 'F': F})

# 連続変数の離散化（構造学習のため）
data['D_disc'] = pd.qcut(data['D'], q=5, labels=False)
data['E_disc'] = pd.qcut(data['E'], q=5, labels=False)
data['F_disc'] = pd.qcut(data['F'], q=5, labels=False)

# 構造学習
hc = HillClimbSearch(data[['A', 'B', 'C', 'D_disc', 'E_disc', 'F_disc']])
best_model = hc.estimate()

# モデルの作成とパラメータ学習
model = BayesianNetwork(best_model.edges())
model.fit(data[['A', 'B', 'C', 'D_disc', 'E_disc', 'F_disc']], estimator=BayesianEstimator)

# 影響度の計算
inference = VariableElimination(model)
influence_dict = {}

for edge in model.edges():
    parent, child = edge
    sensitivity = inference.query([child], evidence={parent: 1})
    sensitivity_diff = sensitivity.values - inference.query([child], evidence={parent: 0}).values
    influence = abs(sensitivity_diff.max())
    influence_dict[edge] = influence

# 正規化された影響度の計算
max_influence = max(influence_dict.values())
min_influence = min(influence_dict.values())
normalized_influence = {edge: (influence - min_influence) / (max_influence - min_influence) 
                        for edge, influence in influence_dict.items()}

# pydotを使用してDAGを描画（影響度を反映）
def plot_dag_pydot_with_influence(model, influence_dict, normalized_influence):
    graph = pydot.Dot(graph_type='digraph', rankdir="LR")
    
    # ノードの追加
    for node in model.nodes():
        if node in ['A', 'B', 'C']:
            graph.add_node(pydot.Node(node, style="filled", fillcolor="lightblue"))
        else:
            graph.add_node(pydot.Node(node.replace('_disc', ''), style="filled", fillcolor="lightgreen"))
    
    # エッジの追加（影響度を反映）
    for edge in model.edges():
        start, end = edge[0].replace('_disc', ''), edge[1].replace('_disc', '')
        influence = influence_dict[edge]
        norm_influence = normalized_influence[edge]
        
        # エッジの色と太さを影響度に基づいて設定
        color = f"#{int(255*(1-norm_influence)):02x}00{int(255*norm_influence):02x}"
        penwidth = 1 + 4 * norm_influence
        
        graph.add_edge(pydot.Edge(start, end, 
                                  label=f"{influence:.3f}",
                                  color=color,
                                  penwidth=penwidth))
    
    # グラフを画像として保存
    graph.write_png("complex_bayesian_network_with_influence.png")
    print("DAG with influence has been saved as 'complex_bayesian_network_with_influence.png'")

# 影響度を反映したDAGの描画
plot_dag_pydot_with_influence(model, influence_dict, normalized_influence)

# パラメータの表示
for node in model.nodes():
    print(f"Parameters for {node}:")
    print(model.get_cpds(node))

# モデル評価 (BICスコアを使用)
from pgmpy.estimators import BicScore

bic = BicScore(data[['A', 'B', 'C', 'D_disc', 'E_disc', 'F_disc']])
bic_score = bic.score(model)
print(f"BIC Score: {bic_score}")

# 推論の例
inference = VariableElimination(model)
print("Probability of C given A=1 and B=1:")
print(inference.query(['C'], evidence={'A': 1, 'B': 1}))

# 感度分析
for node in model.nodes():
    for parent in model.get_parents(node):
        sensitivity = inference.query([node], evidence={parent: 1})
        sensitivity_diff = sensitivity.values - inference.query([node], evidence={parent: 0}).values
        print(f"Sensitivity of {node} to {parent}: {sensitivity_diff.max()}")

# 因果効果の推定 (簡略化した例)
def do_intervention(model, intervention, target):
    modified_model = model.copy()
    modified_model.remove_edges_from([(parent, intervention) for parent in model.get_parents(intervention)])
    inference = VariableElimination(modified_model)
    return inference.query([target], evidence={intervention: 1})

print("Causal effect of A on C:")
print(do_intervention(model, 'A', 'C'))

実行結果は以下です。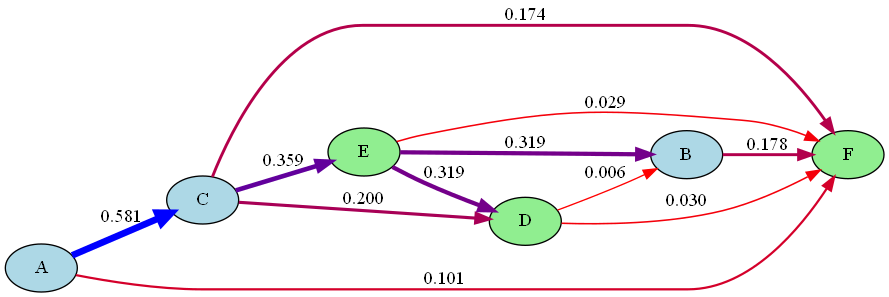今回のDAGに書かれている影響度は、感度分析の一種を使用して、計算しています。すごく簡易的な方法です。なんかLiNGAMの時もロジスティック回帰祭りの時も影響度を載せたDAGを描いていたので、今回もあった方がいいかなと思ったからです。原理的には、親ノード（変数）の値を変化させたときの、子ノードの条件付き確率分布の変化を計算しています。
もっと改善するなら、確率分布の差の絶対値の平均を取る方法やKLダイバージェンスみたいに、二つの確率分布間の距離を情報理論的に測る方法などがあるようです。後段の実装で使う場面があれば使ってみようと思います。因みに、影響度は0から1の範囲に正規化しています。
影響度算出の部分は

sensitivity = inference.query([child], evidence={parent: 1})
sensitivity_diff = sensitivity.values - inference.query([child], evidence={parent: 0}).values
influence = abs(sensitivity_diff.max())

ここです。

動的ベイジアンネットワーク (DBN)

時系列データに対応するため、動的ベイジアンネットワークが導入されました。DBNは、時間の経過に伴う変数の変化を表現します。時刻 $t$ における変数の状態を $X_t$ とすると、モデルは以下のように表されます

$P(X_1, X_2, ..., X_T) = P(X_1) \prod_{t=2}^T P(X_t | X_{t-1}$

ここで、 $T$ は時系列の長さです。

実行コードは以下です

import numpy as np
import pandas as pd
from pgmpy.models import DynamicBayesianNetwork
from pgmpy.estimators import MaximumLikelihoodEstimator
from pgmpy.inference import DBNInference
import pydot
from scipy.stats import entropy

# バージョン情報の出力
import pgmpy
import sys
print(f"pgmpy version: {pgmpy.__version__}")
print(f"Python version: {sys.version}")

# 時系列データの生成関数
def generate_time_series_data(n_samples, n_time_steps):
    data = {}
    
    # 時刻 t での変数生成
    # A: 外部要因（例：経済状況）
    data[('A', 0)] = np.random.binomial(n=1, p=0.6, size=n_samples)
    
    # B: Aに影響される要因（例：企業の業績）
    data[('B', 0)] = np.where(data[('A', 0)] == 1,
                           np.random.binomial(n=1, p=0.7, size=n_samples),
                           np.random.binomial(n=1, p=0.3, size=n_samples))
    
    # C: AとBに影響される要因（例：株価）
    data[('C', 0)] = np.where((data[('A', 0)] == 1) & (data[('B', 0)] == 1),
                           np.random.binomial(n=1, p=0.9, size=n_samples),
                           np.where((data[('A', 0)] == 1) | (data[('B', 0)] == 1),
                                    np.random.binomial(n=1, p=0.5, size=n_samples),
                                    np.random.binomial(n=1, p=0.1, size=n_samples)))
    
    # D: Bに影響される連続変数（例：売上高）
    data[('D', 0)] = np.where(data[('B', 0)] == 1,
                              np.random.normal(loc=100, scale=10, size=n_samples),
                              np.random.normal(loc=80, scale=10, size=n_samples))
    
    # 時刻 t+1 での変数生成
    # A(t+1): A(t)に依存
    data[('A', 1)] = np.where(data[('A', 0)] == 1,
                           np.random.binomial(n=1, p=0.8, size=n_samples),
                           np.random.binomial(n=1, p=0.4, size=n_samples))
    
    # B(t+1): A(t+1)とB(t)に依存
    data[('B', 1)] = np.where((data[('A', 1)] == 1) & (data[('B', 0)] == 1),
                           np.random.binomial(n=1, p=0.9, size=n_samples),
                           np.random.binomial(n=1, p=0.2, size=n_samples))
    
    # C(t+1): A(t+1), B(t+1), C(t)に依存
    data[('C', 1)] = np.where((data[('A', 1)] == 1) & (data[('B', 1)] == 1) & (data[('C', 0)] == 1),
                           np.random.binomial(n=1, p=0.95, size=n_samples),
                           np.random.binomial(n=1, p=0.05, size=n_samples))
    
    # D(t+1): B(t+1)とD(t)に依存
    data[('D', 1)] = 0.7 * data[('D', 0)] + np.where(data[('B', 1)] == 1,
                                                     np.random.normal(loc=30, scale=5, size=n_samples),
                                                     np.random.normal(loc=10, scale=5, size=n_samples))
    
    return pd.DataFrame(data)

# データの生成
np.random.seed(42)  # 再現性のために乱数シードを設定
n_samples = 1000  # サンプル数
n_time_steps = 2  # 時間ステップ数
data = generate_time_series_data(n_samples, n_time_steps)

# 生成されたデータの確認
print("Generated data shape:", data.shape)
print("Generated data columns:", data.columns)

# DBNモデルの定義
dbn = DynamicBayesianNetwork()

# エッジの追加（モデル構造の定義）
dbn.add_edges_from([
    (('A', 0), ('A', 1)),  # A(t) → A(t+1)
    (('A', 0), ('B', 0)),  # A(t) → B(t)
    (('B', 0), ('B', 1)),  # B(t) → B(t+1)
    (('A', 1), ('B', 1)),  # A(t+1) → B(t+1)
    (('A', 0), ('C', 0)),  # A(t) → C(t)
    (('B', 0), ('C', 0)),  # B(t) → C(t)
    (('A', 1), ('C', 1)),  # A(t+1) → C(t+1)
    (('B', 1), ('C', 1)),  # B(t+1) → C(t+1)
    (('C', 0), ('C', 1)),  # C(t) → C(t+1)
    (('B', 0), ('D', 0)),  # B(t) → D(t)
    (('B', 1), ('D', 1)),  # B(t+1) → D(t+1)
    (('D', 0), ('D', 1)),  # D(t) → D(t+1)0
])

# モデルのフィッティング
print("Fitting the model...")
dbn.fit(data, estimator="MLE")
print("Model fitting completed.")

# KLダイバージェンスを用いた影響度の計算関数
def kl_divergence(p, q):
    if isinstance(p, dict) and isinstance(q, dict):
        p = list(p.values())[0]
        q = list(q.values())[0]
    
    if hasattr(p, 'values') and hasattr(q, 'values'):
        p = p.values
        q = q.values
    
    p = np.asarray(p).flatten()
    q = np.asarray(q).flatten()
    if np.sum(p) == 0 or np.sum(q) == 0:
        return 0  # ゼロ除算を避ける
    p = p / np.sum(p)
    q = q / np.sum(q)
    return entropy(p, q)

# 推論エンジンの初期化
inference = DBNInference(dbn)

# 各エッジの影響度を計算
influence_dict = {}
print("Calculating influence for each edge...")
for edge in dbn.edges():
    parent, child = edge
    parent_name, parent_time = parent
    child_name, child_time = child
    
    # 親ノードが0の場合と1の場合の子ノードの条件付き確率を計算
    p_child_given_parent_0 = inference.query(variables=[(child_name, child_time)], evidence={parent: 0})
    p_child_given_parent_1 = inference.query(variables=[(child_name, child_time)], evidence={parent: 1})
    
    # KLダイバージェンスの計算
    try:
        kl_div = kl_divergence(p_child_given_parent_1, p_child_given_parent_0)
        influence_dict[edge] = kl_div
    except Exception as e:
        print(f"Error calculating KL divergence for edge {edge}: {e}")
        influence_dict[edge] = 0  # エラーが発生した場合は影響度を0とする

print("Influence calculation completed.")

# 影響度の正規化
max_influence = max(influence_dict.values())
min_influence = min(influence_dict.values())
normalized_influence = {edge: (influence - min_influence) / (max_influence - min_influence) 
                        if max_influence != min_influence else 0
                        for edge, influence in influence_dict.items()}

# pydotを使用してDAGを描画（影響度を反映）
def plot_dbn_with_influence(dbn, influence_dict, normalized_influence):
    graph = pydot.Dot(graph_type='digraph', rankdir="LR")
    
    # ノードの追加
    for node in dbn.nodes():
        node_name, time = node
        graph.add_node(pydot.Node(f"{node_name}_{time}", style="filled", 
                                  fillcolor="lightblue" if time == 0 else "lightgreen"))
    
    # エッジの追加（影響度を反映）
    for edge in dbn.edges():
        start, end = edge
        start_name, start_time = start
        end_name, end_time = end
        influence = influence_dict[edge]
        norm_influence = normalized_influence[edge]
        
        # NaN チェックと処理
        if np.isnan(norm_influence):
            print(f"Warning: NaN influence for edge {edge}")
            norm_influence = 0  # または他の適切な値

        # エッジの色と太さを影響度に基づいて設定
        try:
            color = f"#{int(255*(1-norm_influence)):02x}00{int(255*norm_influence):02x}"
        except ValueError:
            print(f"Error setting color for edge {edge}. Using default color.")
            color = "#000000"  # デフォルト色を黒に設定
        
        penwidth = 1 + 4 * norm_influence
        
        graph.add_edge(pydot.Edge(f"{start_name}_{start_time}", f"{end_name}_{end_time}", 
                                  label=f"{influence:.3f}",
                                  color=color,
                                  penwidth=penwidth))
    
    # グラフを画像として保存
    graph.write_png("dynamic_bayesian_network_with_influence.png")
    print("DBN with influence has been saved as 'dynamic_bayesian_network_with_influence.png'")

# 影響度を反映したDBNの描画
plot_dbn_with_influence(dbn, influence_dict, normalized_influence)

# 影響度のランキングを表示
print("\nInfluence Ranking:")
sorted_influences = sorted(influence_dict.items(), key=lambda x: x[1], reverse=True)
for i, (edge, influence) in enumerate(sorted_influences, 1):
    print(f"{i}. {edge}: {influence:.4f}")

今回は、影響度の算出にKLダイバージェンスを使用してみました。（0から1に正規化済みです）実行結果は以下です。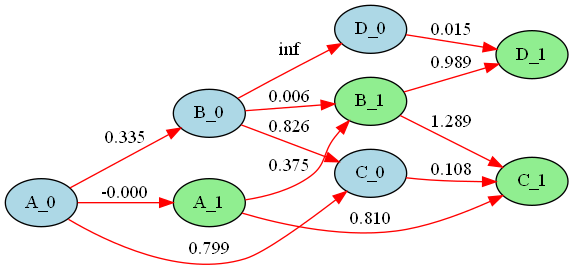いい感じといえばいい感じですかね？もっといいサンプルデータが作れればよかったのですがね...

構造方程式モデル（SEM）の実装

SEMがベイジアンネットワークの一種かといわれると、そうではないのですが、関係性というか類似性があるので、今回取り扱うことにしました。SEMはモデルの定義を分析者が決める必要があり、これまで紹介してきた因果探索手法と異なりますがそこはご認識ください。

SEMは、変数間の関係をより直接的に数学的方程式で表現します。各変数 $X_i$ は、その親変数の関数として表されます

$X_i = f_i(\text{Parents}(X_i), \epsilon_i)$

ここで、 $\epsilon_i$ は誤差項です。SEMは、非線形な関係や介入の効果をモデル化するのに適しています。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
import semopy
print(f"semopy version: {semopy.__version__}")
import pydot
from scipy import stats
import io
from PIL import Image

# サンプルデータの生成
np.random.seed(42)  # 再現性のために乱数シードを設定
n = 1000  # サンプルサイズ

# 潜在変数の生成
latent1 = np.random.normal(0, 1, n)  # 標準正規分布からlatent1を生成
latent2 = 0.5 * latent1 + np.random.normal(0, 0.8, n)  # latent1に依存するlatent2を生成

# 観測変数の生成
# 各観測変数は対応する潜在変数に依存し、ノイズを含む
x1 = latent1 + np.random.normal(0, 0.5, n)
x2 = 1.2 * latent1 + np.random.normal(0, 0.6, n)
x3 = 0.8 * latent1 + np.random.normal(0, 0.4, n)
y1 = latent2 + np.random.normal(0, 0.5, n)
y2 = 1.1 * latent2 + np.random.normal(0, 0.6, n)
y3 = 0.9 * latent2 + np.random.normal(0, 0.4, n)
z = 0.7 * latent1 + 0.6 * latent2 + np.random.normal(0, 0.5, n)  # 両方の潜在変数に依存

# 生成したデータをPandasのDataFrameに格納
data = pd.DataFrame({
    'x1': x1, 'x2': x2, 'x3': x3,
    'y1': y1, 'y2': y2, 'y3': y3,
    'z': z
})

# 構造方程式モデル（SEM）の定義
model = """
    # 測定モデル：潜在変数と観測変数の関係を定義
    latent1 =~ x1 + x2 + x3
    latent2 =~ y1 + y2 + y3
    
    # 構造モデル：潜在変数間の関係と、潜在変数から観測変数zへの関係を定義
    latent2 ~ latent1
    z ~ latent1 + latent2
"""

# モデルの推定
m = semopy.Model(model)  # モデルオブジェクトの作成
r = m.fit(data)  # データを使用してモデルを適合

# 推定結果の表示
print(m.inspect())

# 標準化された係数の取得
std_coeffs = m.inspect()
# 回帰係数と因子負荷量のみを選択
std_coeffs = std_coeffs[std_coeffs['op'].isin(['~', '=~'])]
std_coeffs = std_coeffs[['lval', 'op', 'rval', 'Estimate']]
std_coeffs.columns = ['lval', 'op', 'rval', 'Std.Estimate']

# pydotを使用してDAG（有向非巡回グラフ）を作成
graph = pydot.Dot(graph_type='digraph', rankdir='LR')  # 左から右に配置されるグラフを作成

# グラフにノードを追加
nodes = set(std_coeffs['lval']) | set(std_coeffs['rval'])
for node in nodes:
    if node.startswith('latent'):
        # 潜在変数は水色で表示
        graph.add_node(pydot.Node(node, style="filled", fillcolor="lightblue"))
    else:
        # 観測変数は緑色で表示
        graph.add_node(pydot.Node(node, style="filled", fillcolor="lightgreen"))

# グラフにエッジ（矢印）を追加
min_weight = std_coeffs['Std.Estimate'].abs().min()
max_weight = std_coeffs['Std.Estimate'].abs().max()

for _, row in std_coeffs.iterrows():
    weight = abs(row['Std.Estimate'])
    # 重みを0-1の範囲に正規化
    normalized_weight = (weight - min_weight) / (max_weight - min_weight)
    # 重みに基づいて色を設定（赤から緑）
    color = f"#{int(255*(1-normalized_weight)):02x}00{int(255*normalized_weight):02x}"
    # 重みに基づいて線の太さを設定
    penwidth = 1 + 3 * normalized_weight
    # エッジを追加
    graph.add_edge(pydot.Edge(row['rval'], row['lval'],
                              label=f"{weight:.2f}",
                              color=color,
                              penwidth=penwidth))

# グラフをPNG画像として保存
graph.write_png("sem_dag.png")
print("DAG has been saved as 'sem_dag.png'")

# モデルの適合度指標の計算と表示
fit_indices = semopy.calc_stats(m)
print("\nModel Fit Indices:")
print(fit_indices)

# 標準化された係数の表示
print("\nStandardized Coefficients:")
print(std_coeffs)

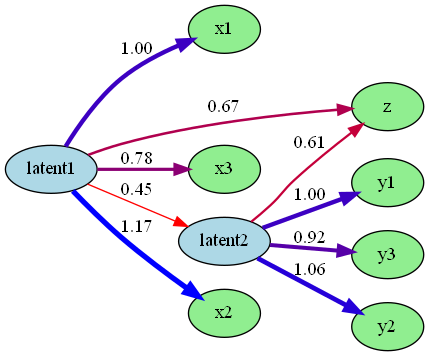
実行結果は以下です。結構良くDAGが描けているように感じますね。今回サンプルデータで作成した、潜在変数は、直接観測や測定することができない、理論的な構成概念のことです。例えば、「知能」や「満足度」、「好意」などです。これらは、関連する観測可能な指標を通じて間接的に測定されます。
というか隠れ変数モデルも実装しようとしてたんですけど、ライブラリの更新かなんかで実装できず... まあ、潜在変数の構造を指定しなければならないんですが、SEMは非線形な関係にも対応できる点も考慮しても結構使える手法そうですね... 私は実務で使用したことが無いので、まだわかりませんが...

最後に

今回のベイジアンネットワークの記事はいかがだったでしょうか？毎回私の記事は、理論に重きを置くとか言っておきながら、実装部分に重きを置いている感じになってしまっているような気がしてなりません。ですが、理論に重きを置きたいものの、私は数学とかに弱く、わかりやすく深く説明しようにも、できないというのが現状です。ただ、手探りで記事を書いていますが、記事を重ねるにつれて、わかりやすい記事が書ければなと思っています。
ベイジアンネットワークって3年前ぐらいから名前だけは知っていたんですが、深く勉強しようとは全然思えなくて、ほったらかしていたので、今回の記事をいい機会に、知見を深められてよかったです。
皆さんがどういった方向の記事を求めているのかに関しても知りたいので、コメントで教えてくれたらななんて思ったりもしてます（笑）今回もお読みいただきありがとうございます。