はじめに

因果探索といえば、最近流れが来ているような、来ていないような微妙な手法ですが、因果推論の流れが来ていることを考えると、計算コストの問題などを解決すれば、意外と流行るのではないかと思い、この記事を書くことにしました。タイトルの通り、因果の強度だけでなく、変数Xが1変化したら変数Yが何変化するのかのような直接効果の算出ができるようにすることは、実務上のキャッチーさとして意外と需要があるのではないかと思ったので、実装にこの要件を含むこととしました。
また、SEMをベースにする理由は、計算効率的な観点から計算コストを減らすために、LiNGAMやベイジアンネットワークなどではなく、SEMをベースとすることにしています。まずは、理論面から内容に入っていきましょう。

SEMCausalExplorerOneHot の理論的背景

1. はじめに

本ドキュメントでは、クラス SEMCausalExplorerOneHot が内包する理論的背景について解説します。従来の構造方程式モデリング(SEM)では因果方向があらかじめ固定されていましたが、本手法は動的に因果方向を探索できるよう拡張した枠組みを採用します。以下では、その理論的基盤となる数式や目的関数、推定アルゴリズムなどを紹介します。

2. SEM の拡張的フレームワーク

$Y_{ij} = \beta_{ij} \cdot D_{ij} \cdot X_i + \epsilon_{ij}$

ここで、 $Y_{ij}$ は変数 $i$ から変数 $j$ への影響を表し、 $\beta_{ij}$ はパス係数（因果強度）、 $D_{ij}$ は方向性パラメータ、 $X_i$ は説明変数、 $\epsilon_{ij}$ は誤差項を示します。 $D_{ij}$ が「因果の向き」を含む連続的な値を持つことで、SEMを拡張しつつ自動で因果方向を推定する枠組みが構成されています。

3. 目的関数の定式化

$\min \sum (Y_{ij} - \beta_{ij} \cdot D_{ij} \cdot X_i)^2 + \lambda_1 \sum|\beta_{ij}| + \lambda_2 \sum|D_{ij}|$

ここではスパース正則化を導入しています。 $\lambda_1$ , $\lambda_2$ はそれぞれ、パス係数と方向性パラメータに対する正則化項の重みです。
不要な経路 $\beta_{ij}$ を抑制しつつ、方向性パラメータ $D_{ij}$ も同様に推定し、方向があいまいな経路を削減する効果があります。

4. 方向性パラメータ $D_{ij}$

$-1 \le D_{ij} \le 1$

$D_{ij}$ は因果方向を表すパラメータで、 $-1$ から $1$ の間を連続的にとります。正の値は順方向 (i → j) の因果、負の値は逆方向 (j → i) の因果を示し、その絶対値が大きいほど方向がはっきりしていることを意味します。
いわば川の流れを表すように、 $D_{ij}$ が正であれば川が i から j に流れ、負であれば j から i に流れると解釈できます。

5. 収束性の保証

$P(\|\hat{\beta} - \beta^*\| < \epsilon) \ge 1 - \delta$

この不等式により、十分なサンプルサイズを用意した場合、推定されたパラメータ $\hat{\beta}$ が真のパラメータ $\beta^*$ に近づく確率が高いことを示します。
データ量が多いほど、誤差 $\epsilon$ の範囲内で推定が行える「信頼度が上がる」というイメージです。

6. 推定アルゴリズム

$\theta_{t+1} = \arg\min_{\theta} \ \mathcal{L}(\theta_t) + \nabla\mathcal{L}(\theta_t)^T(\theta - \theta_t) + \frac{1}{2\eta_t}\|\theta - \theta_t\|^2$

$\theta_t$ は時刻 $t$ でのパラメータ推定値、 $\mathcal{L}(\theta)$ は損失関数（上記の二乗誤差＋正則化項）、 $\eta_t$ はステップサイズを示します。
これは勾配降下法において、更新量を徐々に調整しながら最適解に近づいていく一般的な手法です。SEMCausalExplorerOneHot では、フリップ試行やスコア計算（AIC/BIC）といったステップを組み合わせ、徐々により良い因果構造を探索しています。

7. 因果強度の定量化

$\text{Strength}_{ij} = \bigl|\beta_{ij} \cdot D_{ij}\bigr| \cdot \frac{\sigma_{X_i}}{\sigma_{Y_j}}$

変数 $X_i$ と $Y_j$ のスケール（標準偏差）を考慮しながら、推定されたパス係数と方向性パラメータの積の絶対値で因果強度を定量化しています。
これにより、異なる単位系の変数同士の影響度を比較しやすくなります。

8. 間接効果の計算

$\text{IndirectEffect}_{ij} = \sum_{k \neq i,j} \beta_{ik} \cdot D_{ik} \cdot \beta_{kj} \cdot D_{kj}$

媒介変数を経由する経路（間接経路）の効果を合算したものが間接効果です。
たとえば、 $i$ → $k$ → $j$ のように、一度 $k$ を介して伝わる影響を考慮する場合、上式のように各経路の強度を合計することで間接的な因果影響を推定できます。

9. 不確実性の評価

$\text{CI}_{ij} = \hat{\beta}_{ij} \pm z_{\alpha/2} \sqrt{\text{Var}(\hat{\beta}_{ij})}$

$\hat{\beta}_{ij}$ の推定値に対して、正規分布の臨界値 $z_{\alpha/2}$ を用いた信頼区間を設定することで、不確実性を定量化します。
これは推定結果が「どの程度変動しうるか」を示す指標であり、統計学で一般的に用いられる方法です。

10. モデル選択基準

$\text{IC} = -2 \log \mathcal{L}(\hat{\theta}) + k \log(n)$

$\mathcal{L}(\hat{\theta})$ は対数尤度、 $k$ は推定パラメータ数、 $n$ はサンプル数を表します。これは AIC や BIC のような情報量基準に相当し、よりスパースで適合度の良いモデルを選択するうえで重要な役割を果たします。
SEMCausalExplorerOneHot では、フリップ試行による構造探索と同時にこの基準を計算し、最終的に最も評価の高い因果構造を採用します。

実装

import numpy as np
import pandas as pd
import plotly.graph_objects as go
import warnings

warnings.filterwarnings("ignore")

# Dask for parallel (ローカルin-process)
import dask
import dask.array as da
from dask import delayed

from sklearn.linear_model import Lasso, LogisticRegression
from sklearn.metrics import log_loss

def is_cyclic(adjacency):
    """
    adjacency[i,j] = True => i->j
    DFSで巡回(サイクル)があるか判定 (Trueなら循環あり)
    """
    d = adjacency.shape[0]
    visited = np.zeros(d, dtype=int)

    def dfs(u):
        if visited[u] == 1:
            return True
        if visited[u] == 2:
            return False
        visited[u] = 1
        for v in range(d):
            if adjacency[u,v]:
                if dfs(v):
                    return True
        visited[u] = 2
        return False

    for i in range(d):
        if visited[i]==0:
            if dfs(i):
                return True
    return False

@delayed
def try_flip(X, adjacency_in, i, j, score_before, var_types, alpha, solver_iter, criterion):
    """
    (i,j) のフリップを試し、新しい adjacency を生成し、サイクル or スコア悪化ならNG.
    戻り値: (flip_ok, new_score, new_adj)
    adjacency_in: numpy配列(bool) (immutable想定)
    """
    adj_copy = adjacency_in.copy()
    if adj_copy[i,j]:
        adj_copy[i,j] = False
        adj_copy[j,i] = True
    else:
        adj_copy[j,i] = False
        adj_copy[i,j] = True

    # フリップ後に巡回があれば不採用
    if is_cyclic(adj_copy):
        return (False, score_before, adjacency_in)

    coef_local = estimate_sem_params_local(X, adj_copy, var_types, alpha, solver_iter)
    score_flip = model_score_local(X, adj_copy, coef_local, criterion)

    # スコア悪化も不採用
    if score_flip > score_before:
        return (False, score_before, adjacency_in)
    else:
        return (True, score_flip, adj_copy)

def estimate_sem_params_local(X, adjacency, var_types, alpha, solver_iter):
    """
    adjacency[i,j] => i->j
    binary => logistic-l1(要{0,1}), それ以外=> lasso(continuous)
    """
    d= adjacency.shape[0]
    out= {}
    for j in range(d):
        parents= np.where(adjacency[:, j])[0]
        if len(parents)==0:
            out[j]= {
                "parents": [],
                "coef": None,
                "intercept": None,
                "type": var_types[j]
            }
            continue

        Xp= X[:, parents]
        y= X[:, j]
        vtype= var_types[j]

        # binaryチェック
        if vtype == "binary":
            unq= np.unique(y)
            if len(unq)>2 or not set(unq).issubset({0,1}):
                # fallback => continuous
                vtype="continuous"
            else:
                y= y.astype(int)

        if vtype=="continuous":
            model= Lasso(alpha=alpha, fit_intercept=True, max_iter=solver_iter, random_state=0)
            model.fit(Xp,y)
            out[j]= {
                "parents": parents,
                "coef": model.coef_,
                "intercept": model.intercept_,
                "type": "continuous"
            }
        elif vtype=="binary":
            # logistic-l1
            Cval= 1.0/alpha if alpha>0 else 1e5
            model= LogisticRegression(
                penalty='l1', solver='liblinear', C=Cval,
                max_iter=solver_iter, random_state=0
            )
            model.fit(Xp,y)
            out[j]= {
                "parents": parents,
                "coef": model.coef_[0],
                "intercept": model.intercept_[0],
                "type": "binary"
            }
        else:
            # fallback => continuous
            model= Lasso(alpha=alpha, fit_intercept=True, max_iter=solver_iter, random_state=0)
            model.fit(Xp,y)
            out[j]= {
                "parents": parents,
                "coef": model.coef_,
                "intercept": model.intercept_,
                "type": "continuous"
            }

    return out

def model_score_local(X, adjacency, coef_dict, criterion):
    n, d= X.shape
    loglik=0.0
    n_params=0
    for j in range(d):
        info= coef_dict[j]
        ps= info["parents"]
        if len(ps)==0:
            continue
        c= info["coef"]
        intercept= info["intercept"]
        vtype= info["type"]
        Xp= X[:, ps]
        y= X[:, j]

        if vtype=="continuous":
            yhat= Xp@c + intercept
            sse= np.sum((y-yhat)**2)
            sigma2= sse/n
            if sigma2<1e-12: 
                sigma2=1e-12
            ll_j= - (n/2)*( np.log(2*np.pi*sigma2)+1 )
            loglik+= ll_j
            n_params+= len(c)+2
        elif vtype=="binary":
            z= Xp@c + intercept
            p_= 1/(1+ np.exp(-z))
            nll= log_loss(y, p_, labels=[0,1])
            ll_j= - n*nll
            loglik+= ll_j
            n_params+= len(c)+1
        else:
            yhat= Xp@c + intercept
            sse= np.sum((y-yhat)**2)
            sigma2= sse/n
            if sigma2<1e-12:
                sigma2=1e-12
            ll_j= - (n/2)*(np.log(2*np.pi*sigma2)+1)
            loglik+= ll_j
            n_params+= len(c)+2

    if criterion=="aic":
        score= -2*loglik + 2*n_params
    else:
        score= -2*loglik + n_params*np.log(n)
    return score


class SEMCausalExplorerOneHot:
    def __init__(
        self,
        criterion="bic",
        alpha=0.01,
        max_iter=30,
        solver_iter=500,
        random_state=42,
        dask_scheduler="threads"
    ):
        self.criterion = criterion
        self.alpha = alpha
        self.max_iter = max_iter
        self.solver_iter = solver_iter
        self.random_state = random_state
        self.dask_scheduler = dask_scheduler  # "threads" or "synchronous"

        self.df_encoded_ = None
        self.feature_names_ = None
        self.n_features_ = None
        self.var_types_ = None

        self.adjacency_ = None
        self.coef_dict_ = {}

    def _preprocess(self, df):
        df_clean = df.dropna(axis=0)

        bin_cols= []
        cat_cols= []
        cont_cols= []
        for col in df_clean.columns:
            if pd.api.types.is_numeric_dtype(df_clean[col]):
                unique_vals= df_clean[col].unique()
                if len(unique_vals)==2 and set(unique_vals)=={0,1}:
                    bin_cols.append(col)
                else:
                    cont_cols.append(col)
            else:
                cat_cols.append(col)

        multi_cols= []
        normal_cont_cols= []
        for col in cont_cols:
            unq= df_clean[col].unique()
            if df_clean[col].dtype in [int, np.integer] and len(unq)>2:
                multi_cols.append(col)
            else:
                normal_cont_cols.append(col)

        df_encoded_multi= pd.DataFrame(index=df_clean.index)
        if multi_cols:
            df_to_encode= df_clean[multi_cols]
            if df_to_encode.shape[1]>0:
                df_encoded_multi= pd.get_dummies(df_to_encode, prefix=multi_cols, drop_first=False)

        df_encoded_cat= pd.DataFrame(index=df_clean.index)
        if cat_cols:
            df_cat= df_clean[cat_cols]
            if df_cat.shape[1]>0:
                df_encoded_cat= pd.get_dummies(df_cat, drop_first=False)

        df_remain= df_clean[bin_cols + normal_cont_cols]
        df_final= pd.concat([df_remain, df_encoded_multi, df_encoded_cat], axis=1)

        # floatにそろえる => np.exp等でエラー回避
        df_final= df_final.astype(float)

        var_types= []
        for c in df_final.columns:
            unq= df_final[c].unique()
            if len(unq)==2 and set(unq)=={0.0,1.0}:
                var_types.append("binary")
            else:
                var_types.append("continuous")

        self.df_encoded_= df_final
        self.feature_names_= df_final.columns.tolist()
        self.n_features_= len(self.feature_names_)
        self.var_types_= var_types

        return df_final

    def fit(self, df):
        df_encoded= self._preprocess(df)
        X= df_encoded.values
        d= X.shape[1]

        rng= np.random.default_rng(self.random_state)
        adjacency= np.zeros((d,d), dtype=bool)

        # ここを修正：ランダムなトポロジカル順序に基づいて初期DAGを生成
        perm = rng.permutation(d)
        for idx_i in range(d):
            for idx_j in range(idx_i+1, d):
                i = perm[idx_i]
                j = perm[idx_j]
                # 50%の確率で i->j を生成 (逆方向は張らない)
                if rng.uniform()<0.5:
                    adjacency[i,j]= True

        # 念のため初期化段階で循環がないかチェック
        assert not is_cyclic(adjacency), "初期化段階で巡回が発生しました(想定外)."

        best_score= np.inf
        best_adj= adjacency.copy()
        best_coef= {}

        old_adj= adjacency.copy()

        for iteration in range(self.max_iter):
            local_coef= estimate_sem_params_local(X, adjacency, self.var_types_, self.alpha, self.solver_iter)
            score_curr= model_score_local(X, adjacency, local_coef, self.criterion)

            if score_curr< best_score:
                best_score= score_curr
                best_adj= adjacency.copy()
                best_coef= local_coef

            tasks= []
            pairs= []
            for i2 in range(d):
                for j2 in range(i2+1,d):
                    # どちらか一方だけ辺がある場合にのみフリップ試行
                    if adjacency[i2,j2] == adjacency[j2,i2]:
                        continue
                    adj_in= adjacency.copy()
                    t= try_flip(
                        X, adj_in, i2, j2, score_curr,
                        self.var_types_, self.alpha, self.solver_iter,
                        self.criterion
                    )
                    tasks.append(t)
                    pairs.append((i2,j2))

            # Daskで並列実行
            results= dask.compute(*tasks, scheduler=self.dask_scheduler)

            changed=0
            for (flip_ok, new_score, new_adj), (i2,j2) in zip(results, pairs):
                if flip_ok:
                    changed+=1
                    score_curr= new_score
                    adjacency= new_adj

            diff= np.sum(adjacency!= old_adj)
            if diff==0:
                # もう更新がなければ打ち切り
                break
            old_adj= adjacency.copy()

        # 学習終了 => ベスト確定
        self.adjacency_= best_adj
        self.coef_dict_= best_coef

        # 念のため最終的なグラフに循環がないかチェック
        assert not is_cyclic(self.adjacency_), "最終的なグラフに循環が発生しています。"

        return self

    def plot_causal_graph(self, threshold=0.01, radius_scale=2.0, fig_width=900, fig_height=900):
        if self.adjacency_ is None:
            raise RuntimeError("Model not fitted yet.")

        d= self.n_features_
        angle_step= 2*np.pi/d
        positions= [
            (radius_scale*np.cos(i*angle_step), radius_scale*np.sin(i*angle_step)) 
            for i in range(d)
        ]

        node_x= [p[0] for p in positions]
        node_y= [p[1] for p in positions]
        node_trace= go.Scatter(
            x=node_x, 
            y=node_y,
            mode='markers+text',
            text=self.feature_names_,
            textposition='bottom center',
            marker=dict(size=20, color='lightblue', line=dict(color='black', width=1)),
            hoverinfo='text'
        )

        annotations=[]
        edge_list = []

        for j, info in self.coef_dict_.items():
            ps= info["parents"]
            if ps is None or len(ps)==0:
                continue
            c= info["coef"]
            if c is None: 
                continue
            vtype= info["type"]

            abscoef= np.abs(c) if c.ndim==1 else np.abs(c.ravel())

            for ip, par in enumerate(ps):
                strength= abscoef[ip]
                edge_list.append({
                    "source": self.feature_names_[par],
                    "target": self.feature_names_[j],
                    "coefficient": c[ip],
                    "vtype": vtype
                })
                if strength< threshold:
                    continue

                x0, y0= positions[par]
                x1, y1= positions[j]

                annotations.append(
                    dict(
                        x=x1, y=y1,
                        ax=x0, ay=y0,
                        xref='x', yref='y',
                        axref='x', ayref='y',
                        text="",
                        showarrow=True,
                        arrowhead=3,
                        arrowwidth=2,
                        arrowcolor='#555',
                        standoff=5
                    )
                )
                mx= (x0+x1)/2
                my= (y0+y1)/2
                dx= x1-x0
                dy= y1-y0
                length= np.sqrt(dx*dx+ dy*dy)+1e-12
                nx= -dy/ length
                ny= dx/ length
                offset_scale= 0.07
                ox= mx+ offset_scale*nx
                oy= my+ offset_scale*ny

                annotations.append(
                    dict(
                        x= ox, y= oy,
                        xref='x', yref='y',
                        showarrow=False,
                        text= f"{c[ip]:.3f}",
                        font=dict(color="#333", size=12)
                    )
                )

        fig= go.Figure(
            data=[node_trace],
            layout=go.Layout(
                title="Estimated Causal Graph",
                showlegend=False,
                xaxis=dict(showgrid=False, zeroline=False, showticklabels=False),
                yaxis=dict(showgrid=False, zeroline=False, showticklabels=False),
                margin=dict(l=40, r=40, b=40, t=80),
                width=fig_width,
                height=fig_height,
                annotations=annotations
            )
        )
        fig.show()

        edge_df = pd.DataFrame(edge_list)
        if not edge_df.empty:
            print("=== Causal Edges with Coefficients ===")
            display(edge_df)
            edge_df.to_csv("Causal_Edges.csv", index=False)
        else:
            print("No edges with coefficient above the threshold.")

    def simulate_intervention(self, df, from_idx, delta=1.0, steps=5):
        if self.adjacency_ is None:
            raise RuntimeError("Model not fitted yet.")
        df_enc= self.df_encoded_.dropna(axis=0)
        X_= df_enc.values
        baseline= X_.mean(axis=0)
        new_values= baseline.copy()
        new_values[from_idx]+= delta

        d= self.n_features_
        for _ in range(steps):
            updated= False
            for j in range(d):
                info= self.coef_dict_[j]
                ps= info["parents"]
                if len(ps)==0:
                    continue
                c= info["coef"]
                intercept= info["intercept"]
                vtype= info["type"]
                old_val= new_values[j]

                pvals= new_values[ps]
                if vtype=="continuous":
                    val= intercept+ np.sum(c*pvals)
                    new_values[j]= val
                elif vtype=="binary":
                    z= intercept+ np.sum(c*pvals)
                    p_= 1/(1+ np.exp(-z))
                    new_values[j]= p_
                else:
                    val= intercept+ np.sum(c*pvals)
                    new_values[j]= val

                if abs(old_val- new_values[j])>1e-8:
                    updated= True
            if not updated:
                break
        return baseline, new_values

    def plot_intervention_result(
        self, df, from_idx, delta=1.0, steps=5, threshold=0.01,
        radius_scale=2.0, fig_width=900, fig_height=900
    ):
        baseline, new_val= self.simulate_intervention(df, from_idx, delta, steps)
        diff= new_val- baseline

        d= self.n_features_
        angle_step= 2*np.pi/d
        positions= [
            (radius_scale*np.cos(i*angle_step), radius_scale*np.sin(i*angle_step)) 
            for i in range(d)
        ]

        node_x= [p[0] for p in positions]
        node_y= [p[1] for p in positions]
        node_color= diff
        node_labels= []
        for i, nm in enumerate(self.feature_names_):
            node_labels.append(f"{nm}\n(Δ={diff[i]:.3f})")

        node_trace= go.Scatter(
            x=node_x, 
            y=node_y,
            mode='markers+text',
            text=node_labels,
            textposition='bottom center',
            marker=dict(
                colorscale='RdBu',
                cmin=node_color.min(),
                cmax=node_color.max(),
                color=node_color,
                size=25,
                showscale=True,
                colorbar=dict(title="Change")
            ),
            hoverinfo='text'
        )

        annotations=[]
        for j, info in self.coef_dict_.items():
            ps= info["parents"]
            if ps is None or len(ps)==0: 
                continue
            c= info["coef"]
            if c is None: 
                continue
            vtype= info["type"]
            abscoef= np.abs(c) if c.ndim==1 else np.abs(c.ravel())

            for ip, par in enumerate(ps):
                strength= abscoef[ip]
                if strength< threshold:
                    continue
                x0, y0= positions[par]
                x1, y1= positions[j]

                annotations.append(
                    dict(
                        x=x1, y=y1,
                        ax=x0, ay=y0,
                        xref='x', yref='y',
                        axref='x', ayref='y',
                        text="",
                        showarrow=True,
                        arrowhead=3,
                        arrowwidth=2,
                        arrowcolor='#555',
                        standoff=5
                    )
                )
                mx= (x0+x1)/2
                my= (y0+y1)/2
                dx= x1-x0
                dy= y1-y0
                length= np.sqrt(dx*dx+ dy*dy)+1e-12
                nx= -dy/ length
                ny= dx/ length
                offset_scale= 0.07
                ox= mx+ offset_scale*nx
                oy= my+ offset_scale*ny

                annotations.append(
                    dict(
                        x=ox, y=oy,
                        xref='x', yref='y',
                        showarrow=False,
                        text=f"{c[ip]:.3f}",
                        font=dict(color="#333", size=12)
                    )
                )

        fig= go.Figure(
            data=[node_trace],
            layout=go.Layout(
                title=f"Intervention on {self.feature_names_[from_idx]} +{delta}",
                showlegend=False,
                xaxis=dict(showgrid=False, zeroline=False, showticklabels=False),
                yaxis=dict(showgrid=False, zeroline=False, showticklabels=False),
                margin=dict(l=40,r=40,b=40,t=80),
                width=fig_width,
                height=fig_height,
                annotations=annotations
            )
        )
        fig.show()

        result_df = pd.DataFrame({
            "Feature": self.feature_names_,
            "Baseline": baseline,
            "New Values": new_val,
            "Diff": diff
        })
        print("=== Intervention Result ===")
        display(result_df)
        result_df.to_csv("intervention_Result.csv", index=False)

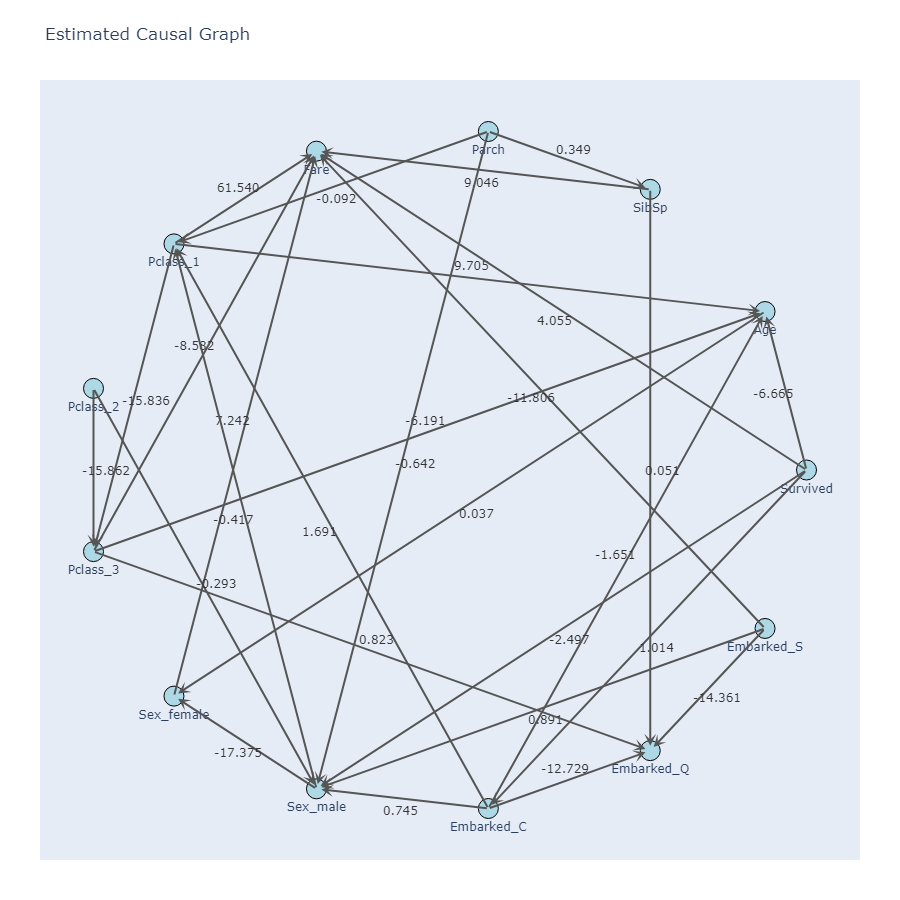
タイタニックのデータで因果グラフを作ってみた結果が以下です。

df = pd.read_csv("train.csv")
df = df[["Survived", "Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked"]]
df["Pclass"] = df["Pclass"].astype("str")

model= SEMCausalExplorerOneHot(
    criterion="bic",
    alpha=0.05,
    max_iter=15,
    solver_iter=300,
    random_state=42,
    # ローカルスレッドで計算(分散クラスターを立ち上げない)
    dask_scheduler="threads"
)
model.fit(df)
model.plot_causal_graph(threshold=0.02)

from_idx= 1
model.plot_intervention_result(df, from_idx= from_idx, delta=1.0, steps=5, threshold=0.02)

ageを1変化させたときの他の変数の変化は以下です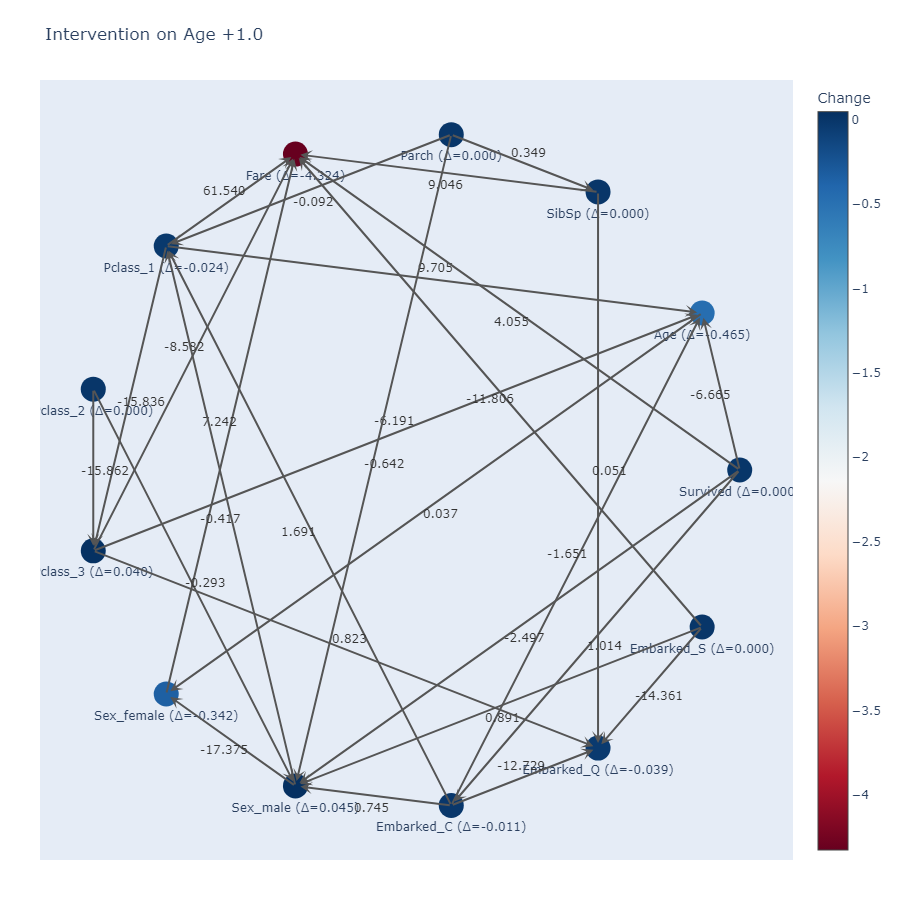このように実際に因果探索を行わせてみると、エッジの方向がドメイン知識と明らかに異なっている部分は出てきてしまっていますが、ageを1変化させたときの他の変数の変化は一定納得がいく部分も一部アリといった感じです。

まとめ

以上のように、SEMCausalExplorerOneHot では、拡張された SEM の枠組みに基づいて因果方向を自動的に探索し、スパース推定や情報量基準の活用によって不要な経路を削除しながら学習を行います。
さらに、Dask を用いた並列計算を組み合わせることで大規模データでも効率的に因果構造を推定できるよう工夫されています。
このような理論的背景のもと、得られたモデルは循環がなく、かつ適切な方向を持つ DAG 構造として表現されます。

SEMをベースにしていることや、二値を扱えたり、多クラス変数を扱えるようにしている部分で、DAGの厳密性などを満たす処理が実装できなかったので、どんなデータでも扱えるようにという制約を外せば、もっと厳密性のあるDAGを生成できるクラスが作れそうでした。
ということで今回の結果は、分析の初手に回してみる程度であれば有用なのかな？と感じる程度の手ごたえでした。

tomtom58’s blog

SEMを拡張して変数Xが1変化したら因果先変数が何変化するのかまで出せる因果探索手法を考えたい