合成コントロール法の理論と実装

因果推論 DID

はじめに

結構前は、DIDに関する記事から、はてなブログを書き始めたので、久々にDIDに関する記事を書いてみようかなということで、今回は合成コントロール法に焦点を当てていきたいと思います。今回も恒例の様に、理論の説明と、実装両方扱っていきたいと思います。また、サンプルデータ（できうる限り複雑なものにするつもり）で合成コントロール法とCausal Impactどっちがいい結果を出したのか、後は以前解説した傾向スコアで行うDIDとも比較できたらなと書いている初期は思っております。
どうなるかは、まだ自分にはわかっていません。
今回の記事は、厳密にいこうということで、論文を基に理論部分は進めていきます。
これが参考にする論文です。有名な奴ですね。

合成コントロール法

合成コントロール法は、従来のDID（差分の差分法）を拡張した手法です。この手法の主な特徴と理論的な背景は以下のとおりです。
　　
合成コントロール法では、以下のようなモデルを考えます

Y^N_{it} = \delta_t + \theta_t Z_i + \lambda_t \mu_i + \varepsilon_{it}

ここで

Y^N_{it} は介入がない場合の $i$ 地域の $t$ 期のアウトカム
\delta_t は時間固定効果
Z_i は観察可能な共変量ベクトル
\theta_t はその係数ベクトル
\lambda_t は観察不可能な共通要因ベクトル
\mu_i は地域固有の要因負荷ベクトル
\varepsilon_{it} は誤差項

　　

このモデルは、通常のDIDモデルを一般化したものと考えられます。従来のDIDでは \lambda_t が時間を通じて一定であることを仮定していましたが、合成コントロール法ではこの仮定を緩和し、時間変動を許容しています。

　　
実際に合成コントロールの構築を考えます。処置を受けた地域（例：カリフォルニア州）のアウトカムを、処置を受けていない地域（ドナープール）の加重平均で近似します

\sum_{j=2}^{J+1} w_j Y_{jt}
ここで w_j は各コントロール地域に割り当てられる重みで、非負で合計が1となる制約があります。

　　
重みの推定に関して説明していきたいと思います。最適な重みは、処置前期間のアウトカムと予測変数の値が処置地域と合成コントロールで可能な限り近くなるように選択されます。

\sum_{j=2}^{J+1} w^j Y{j1} = Y_{11}, \ldots, \sum_{j=2}^{J+1} w^j Y{jT_0} = Y_{1T_0}
\sum_{j=2}^{J+1} w^*_j Z_j = Z_1

これらの条件を満たす重みを見つけることで、観察可能な特性と観察不可能な要因の両方について、処置地域と合成コントロールを可能な限り近づけることができます。

早速処置効果の推定の内容に入っていきましょう。処置効果は、処置後期間における実際の処置地域のアウトカムと合成コントロールのアウトカムの差として推定されます。

\hat{\alpha}{1t} = Y{1t} - \sum_{j=2}^{J+1} w^*j Y{jt} (t > T_0)

この方法の利点は、時間変動する未観測の交絡要因をコントロールできることです。また、比較対象となる合成コントロールの構成が明示的であり、外挿を避けられるという特徴があります。
ここまででわかったように、処置群に近しいものを作るために、適切な重みで加重平均をとって、対照群となるものを作るのが、合成コントロール法というわけです。最後の話だけでも理解できればいいと思います。
もう少し解説すると、合成コントロール法は、処置群（介入を受けた地域や単位）と可能な限り類似した特性を持つ「合成的な」対照群を作り出す手法です。この合成対照群は、処置を受けていない複数の単位（ドナープール）の加重平均として構築されます。合成コントロール法の目的は、処置前の期間において処置群と可能な限り類似したトレンドを示す対照群を作ることです。これにより、処置がなかった場合に処置群がたどったであろう仮想的な経路（反事実）を推定します。各ドナー単位に割り当てられる重みは、処置前の期間における処置群の特性（アウトカム変数の値や他の予測変数）を最もよく再現するように決定されます。これは最適化問題として解かれます。ということで、重みの決定がデータに基づいて行われるため、主観による比較になりずらいという利点があるわけです。

実装

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# ランダムシードを設定（再現性のため）
np.random.seed(123)

# パラメータ設定
n_units = 50  # 総単位数
n_treated = 3  # 処置を受ける単位数
n_time = 100  # 時点数
treatment_time = 60  # 処置が開始される時点

# 時間変数の生成
time = np.arange(n_time)

# 非線形時間トレンドの生成（全ユニットに共通）
nonlinear_trend = 10 * np.sin(time / 10) + time / 10

# データフレームの作成
data = pd.DataFrame({
    'unit': np.repeat(range(1, n_units + 1), n_time),
    'time': np.tile(time, n_units)
})

# ユニット固有の効果を生成（各ユニットに固有の切片）
unit_effects = np.random.normal(0, 5, n_units)

# 季節性の生成（ユニットごとに異なる周期性）
seasonality = np.array([np.sin(2 * np.pi * (time + shift) / 12) for shift in np.random.rand(n_units)])
seasonality = seasonality.flatten()

# 共変量の生成
data['X1'] = np.random.normal(0, 1, len(data)) + data['unit'] * 0.1  # ユニットに依存する連続変数
data['X2'] = np.random.uniform(0, 1, len(data)) + np.sin(data['time'] / 10)  # 時間に依存する連続変数
data['X3'] = np.random.poisson(5, len(data)) + data['unit'] * 0.2  # ユニットに依存するカウント変数
data['X4'] = np.random.choice(['A', 'B', 'C'], len(data))  # カテゴリカル変数

# X4のダミー変数を作成
X4_dummies = pd.get_dummies(data['X4'], prefix='X4')
data = pd.concat([data, X4_dummies], axis=1)

# アウトカム変数の生成
data['Y'] = (50 +  # ベースライン
             unit_effects[data['unit'] - 1] +  # ユニット固有効果
             nonlinear_trend[data['time']] +  # 非線形時間トレンド
             5 * seasonality +  # 季節性
             2 * data['X1'] +  # X1の効果
             3 * data['X2'] +  # X2の効果
             0.5 * data['X3'] +  # X3の効果
             1 * data['X4_A'] +  # X4_Aの効果
             2 * data['X4_B'] +  # X4_Bの効果
             np.random.normal(0, 2, len(data)))  # ランダムノイズ

# 真の処置効果を計算する関数
def true_treatment_effect(t, treatment_time):
    return 10 * (1 - np.exp(-(t - treatment_time) / 20)) if t >= treatment_time else 0

# 処置効果を追加（最初の3ユニットのみ）
treatment_effect = np.array([true_treatment_effect(t, treatment_time) for t in data['time']])
data.loc[(data['unit'] <= n_treated) & (data['time'] >= treatment_time), 'Y'] += treatment_effect[(data['unit'] <= n_treated) & (data['time'] >= treatment_time)]

# データを処置前と処置後に分割
pre_treatment = data[data['time'] < treatment_time]
post_treatment = data[data['time'] >= treatment_time]

# 処置群と対照群に分割
treated_units = pre_treatment[pre_treatment['unit'] <= n_treated]
control_units = pre_treatment[pre_treatment['unit'] > n_treated]

# 予測変数の平均を計算
predictors = ['X1', 'X2', 'X3', 'X4_A', 'X4_B']
X_treated = treated_units.groupby('unit')[predictors].mean()
X_control = control_units.groupby('unit')[predictors].mean()

# 処置前期間の結果変数
Y_treated = treated_units.pivot(index='time', columns='unit', values='Y')
Y_control = control_units.pivot(index='time', columns='unit', values='Y')

# 合成コントロールの重みを最適化する関数
def get_w(X, X1, Y, Y1):
    def loss(w):
        return np.sqrt(np.mean((Y1 - Y.dot(w))**2))
    
    cons = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1},)  # 重みの合計が1になる制約
    bounds = [(0, 1) for _ in range(X.shape[0])]  # 各重みが0以上1以下という制約
    w0 = np.ones(X.shape[0]) / X.shape[0]  # 初期値は均等な重み
    
    res = minimize(loss, w0, method='SLSQP', constraints=cons, bounds=bounds)
    return res.x

# 各処置ユニットに対して合成コントロールを作成
treatment_effects = []
true_effects = []
for treated_unit in range(1, n_treated + 1):
    # 重みの計算
    w = get_w(X_control, X_treated.loc[treated_unit], Y_control, Y_treated[treated_unit])
    
    # 合成コントロールの作成（処置後期間も含む）
    Y_synthetic = pd.concat([Y_control, post_treatment[post_treatment['unit'] > n_treated].pivot(index='time', columns='unit', values='Y')]).dot(w)
    
    # 処置後期間の実際の値と合成コントロールの値
    Y_treated_all = data[data['unit'] == treated_unit].set_index('time')['Y']
    
    # 処置効果の計算
    effect = np.mean(Y_treated_all[treatment_time:] - Y_synthetic[treatment_time:])
    treatment_effects.append(effect)
    
    # 真の処置効果の計算
    true_effect = np.mean([true_treatment_effect(t, treatment_time) for t in range(treatment_time, n_time)])
    true_effects.append(true_effect)
    
    # 処置がなかった場合の仮想的な結果を計算
    Y_treated_without_treatment = Y_treated_all.copy()
    Y_treated_without_treatment[treatment_time:] -= np.array([true_treatment_effect(t, treatment_time) for t in Y_treated_without_treatment.index[treatment_time:]])
    
    # 結果のプロット
    plt.figure(figsize=(12, 6))
    plt.plot(Y_treated_all.index, Y_treated_all, label='Treated (Actual)', color='blue')
    plt.plot(Y_synthetic.index, Y_synthetic, label='Synthetic Control', color='red')
    plt.plot(Y_treated_without_treatment.index, Y_treated_without_treatment, label='Treated (Without Intervention)', color='blue', linestyle='--')
    plt.axvline(x=treatment_time, color='green', linestyle='--', label='Treatment Time')
    plt.xlabel('Time')
    plt.ylabel('Outcome')
    plt.legend()
    plt.title(f'Synthetic Control Method - Unit {treated_unit}')
    plt.show()

    # 処置効果のプロット
    plt.figure(figsize=(12, 6))
    treatment_effect = Y_treated_all - Y_treated_without_treatment
    plt.plot(treatment_effect.index, treatment_effect, label='Treatment Effect', color='purple')
    plt.axvline(x=treatment_time, color='green', linestyle='--', label='Treatment Time')
    plt.axhline(y=0, color='black', linestyle='--')
    plt.xlabel('Time')
    plt.ylabel('Treatment Effect')
    plt.legend()
    plt.title(f'Treatment Effect - Unit {treated_unit}')
    plt.show()

print("Estimated treatment effects vs True effects:")
for i, (est_effect, true_effect) in enumerate(zip(treatment_effects, true_effects), 1):
    print(f"Unit {i}: Estimated = {est_effect:.4f}, True = {true_effect:.4f}")

# プラセボテストの実行
placebo_effects = []
for unit in range(n_treated + 1, n_units + 1):
    # 各非処置ユニットを仮想的な処置ユニットとして扱う
    placebo_treated = pre_treatment[pre_treatment['unit'] == unit]
    placebo_control = pre_treatment[(pre_treatment['unit'] != unit) & (pre_treatment['unit'] > n_treated)]
    
    X_placebo_treated = placebo_treated[predictors].mean()
    X_placebo_control = placebo_control.groupby('unit')[predictors].mean()
    
    Y_placebo_treated = placebo_treated.pivot(index='time', columns='unit', values='Y').iloc[:, 0]
    Y_placebo_control = placebo_control.pivot(index='time', columns='unit', values='Y')
    
    # プラセボユニットの合成コントロールの重みを計算
    w_placebo = get_w(X_placebo_control, X_placebo_treated, Y_placebo_control, Y_placebo_treated)
    
    # プラセボユニットの合成コントロールを作成
    Y_placebo_synthetic = pd.concat([Y_placebo_control, post_treatment[(post_treatment['unit'] != unit) & (post_treatment['unit'] > n_treated)].pivot(index='time', columns='unit', values='Y')]).dot(w_placebo)
    
    Y_placebo_treated_all = data[data['unit'] == unit].set_index('time')['Y']
    
    # プラセボ効果の計算
    placebo_effect = np.mean(Y_placebo_treated_all[treatment_time:] - Y_placebo_synthetic[treatment_time:])
    placebo_effects.append(placebo_effect)

# プラセボテストの結果をプロット
plt.figure(figsize=(12, 6))
plt.hist(placebo_effects, bins=20, alpha=0.5, label='Placebo Effects')
for est_effect, true_effect in zip(treatment_effects, true_effects):
    plt.axvline(x=est_effect, color='r', linestyle='--', label='Estimated Effect')
    plt.axvline(x=true_effect, color='g', linestyle='--', label='True Effect')
plt.axvline(x=np.mean(treatment_effects), color='r', linestyle='-', label='Mean Estimated Effect')
plt.axvline(x=np.mean(true_effects), color='g', linestyle='-', label='Mean True Effect')
plt.xlabel('Treatment Effect')
plt.ylabel('Frequency')
plt.legend()
plt.title('Distribution of Placebo Effects')
plt.show()

# p値の計算
p_values = [(np.sum(np.abs(placebo_effects) >= np.abs(effect)) + 1) / (len(placebo_effects) + 1) for effect in treatment_effects]
print("\np-values:")
for i, p_value in enumerate(p_values, 1):
    print(f"Unit {i}: {p_value:.4f}")

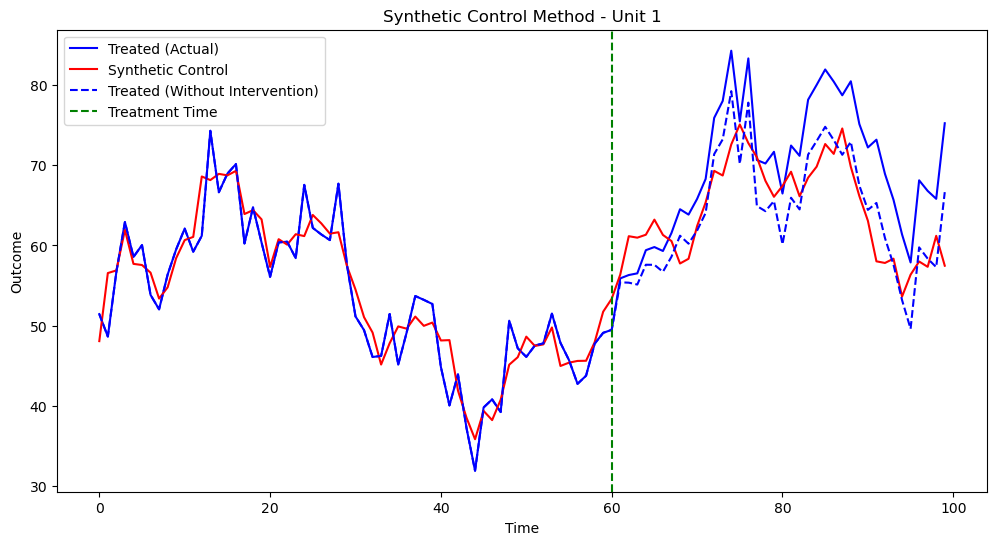
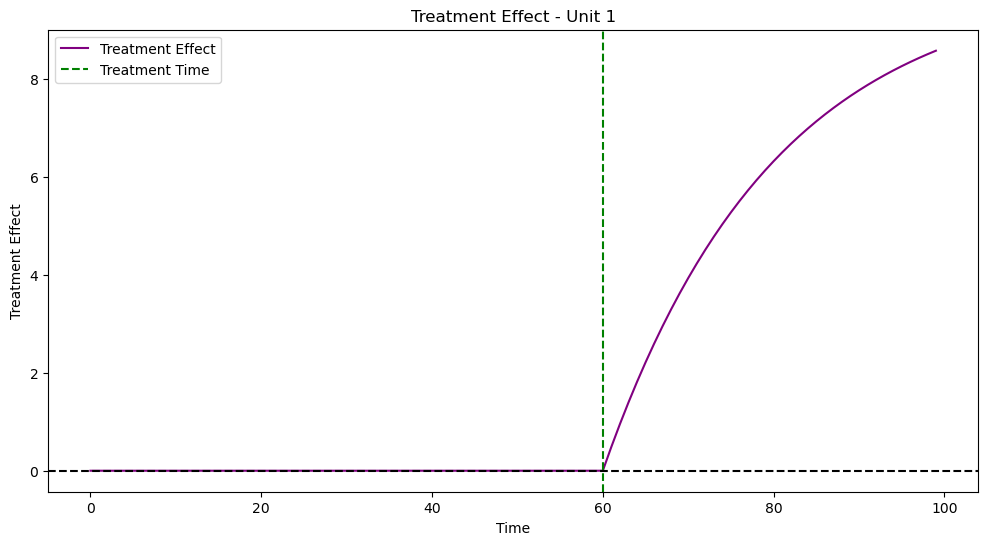
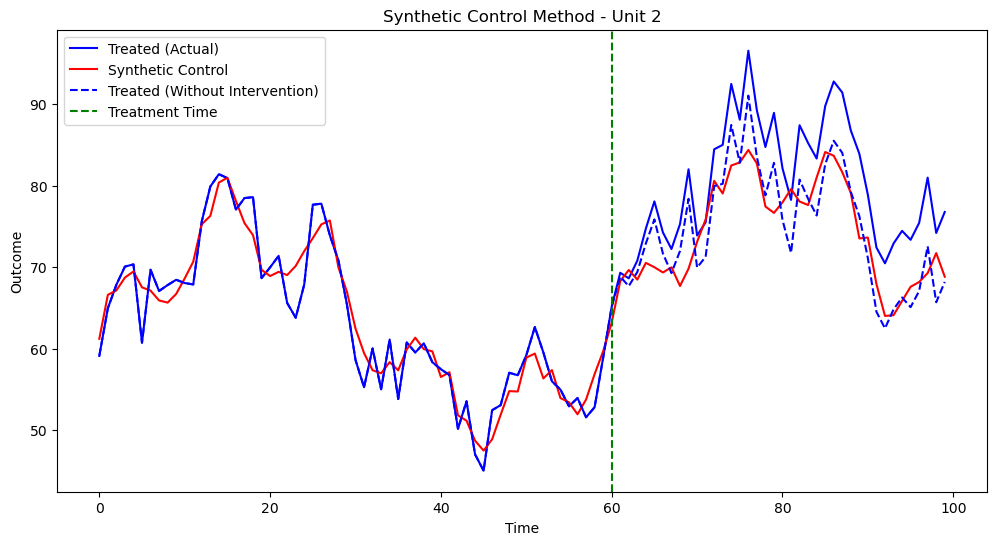
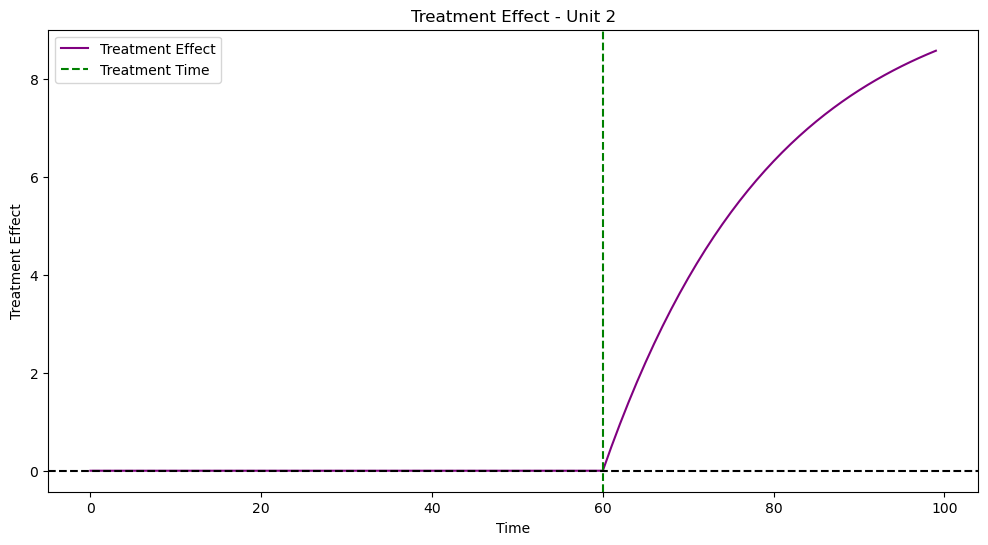
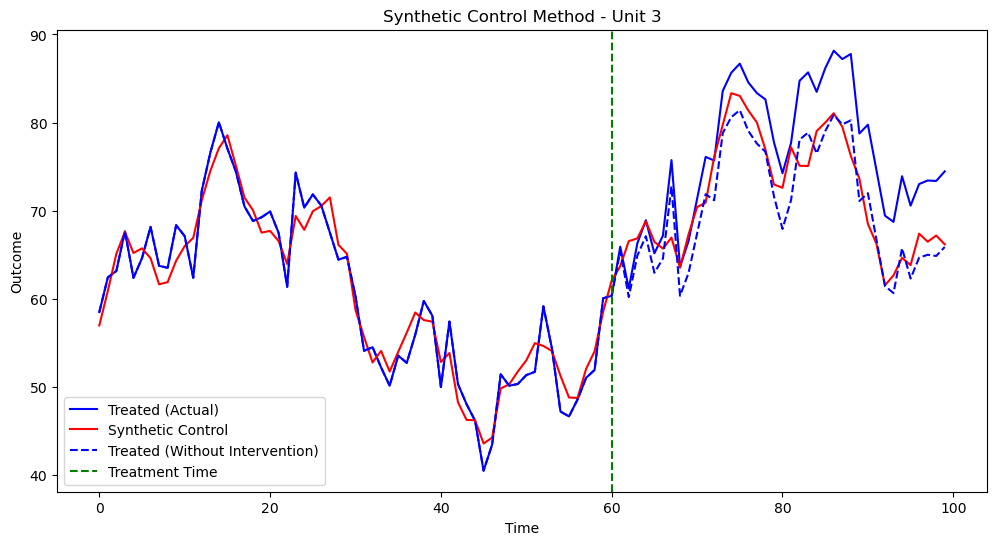
実行結果は以下です 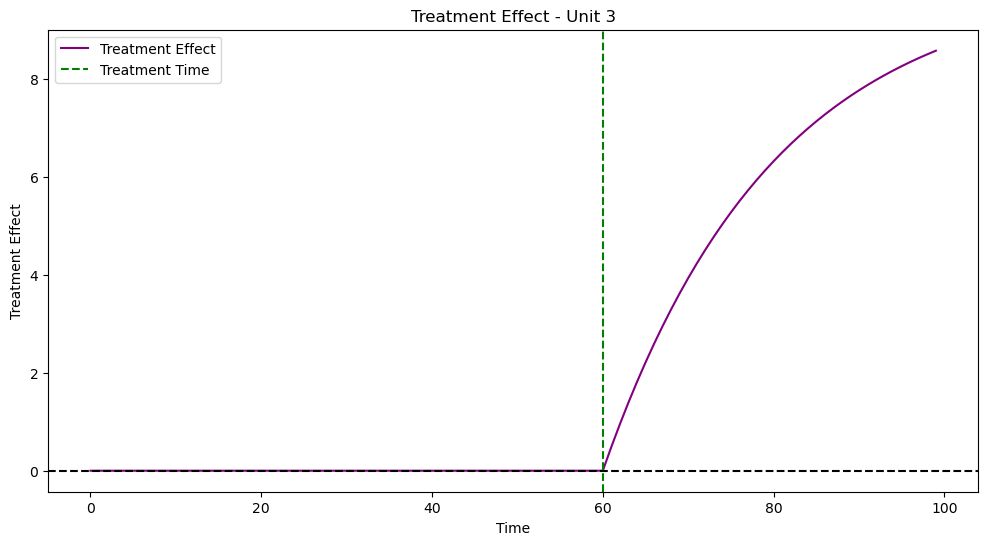結構いい感じに反事実のトレンドが作れているのではないでしょうか？ 次にプラセボテストというものを今回しているので、その結果も観ていきましょう。プラセボテストとは合成コントロール法の結果の信頼性を確認するための手法です。このテストでは、実際には処置を受けていない単位（国や地域など）に対して、架空の処置効果を推定します。具体的には、処置を受けていない各単位をあたかも処置を受けたかのように扱い、合成コントロール法を適用して「処置効果」を計算します。本来、これらの単位では効果がゼロに近いはずです。多くの単位で効果がゼロ付近に集中していれば、方法の信頼性が高いと判断できます。実際の処置単位の推定効果をこれらのプラセボ効果の分布と比較し、大きく外れていれば、その効果は統計的に意味があると考えられます。 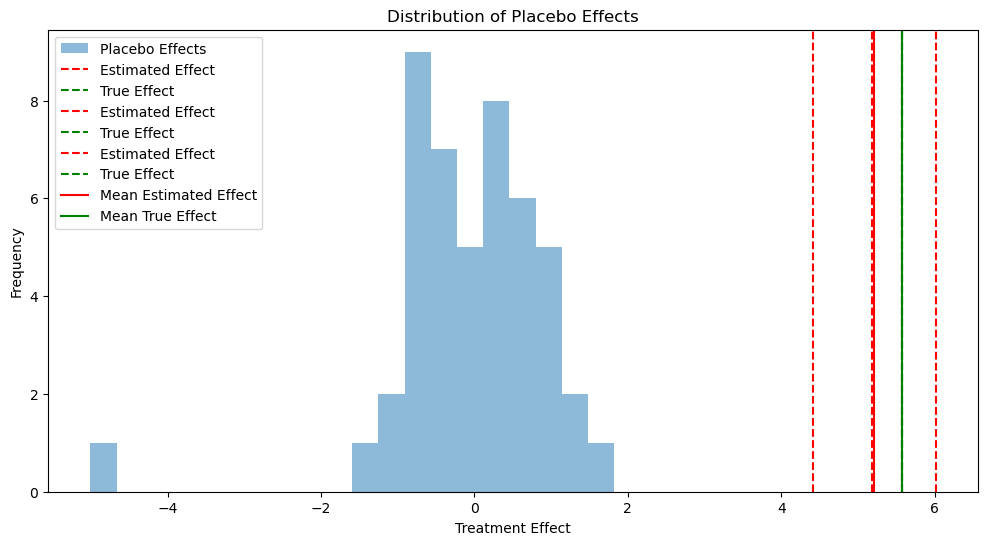結果のとらえ方ですが、 青いヒストグラムは、処置を受けていない単位（プラセボ群）に対して計算された見かけの「処置効果」の分布を示しています。これらの効果は本来ゼロ周辺に集中するはずです。 赤い破線は、実際に処置を受けた単位に対して推定された処置効果を示しています。3本の赤い破線は、3つの処置単位それぞれの推定効果を表しています。
緑の破線は、シミュレーションで設定された真の処置効果を示しています。
実線の赤（推定平均効果）と緑（真の平均効果）は、それぞれ推定効果と真の効果の平均値を示しています。
推定された処置効果（赤い破線）がプラセボ効果の分布（青いヒストグラム）から大きく離れているほど、その効果が統計的に有意であることを示唆します。
今回の結果を見てみると、プラセボ効果の分布から明確に離れているので、処置効果は統計的に有意であると言えるでしょう。ただ、推定された効果は真の効果に近いが、若干過小評価している傾向にあることがうかがえます。また、プラセボ効果はほぼゼロ周辺に集中しており、合成コントロール法が適切に機能していると言えるでしょう。
ここまでで、合成コントロール法の実行結果の説明は以上です。 付録というか要望のあった件に関して次に書いていきます

付録（合成コントロール法とCausal Impactの比較＋前に解説した傾向スコアを用いる方法も追加で）

Causal Impactはtfcausalimpactを使用しています。causalimpactはスパイクスラブ分布が実装されていないみたいな話があったので、tfcausalimpactを選択しています。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from sklearn.linear_model import LogisticRegression
from statsmodels.formula.api import wls
from causalimpact import CausalImpact
from datetime import datetime, timedelta

# ランダムシードを設定（再現性のため）
np.random.seed(12345)

# パラメータ設定
n_units = 20
n_treated = 1
n_time = 200
treatment_time = 150

# 時間変数の生成
time = np.arange(n_time)

# データフレームの作成
data = pd.DataFrame({
    'unit': np.repeat(range(1, n_units + 1), n_time),
    'time': np.tile(time, n_units)
})

# 共変量の生成（増やす）
data['X1'] = np.random.normal(0, 1, len(data)) + 0.05 * data['time']
data['X2'] = np.random.uniform(0, 1, len(data)) + 0.03 * np.sin(data['time'] / 10)
data['X3'] = np.random.poisson(3, len(data)) + 0.01 * data['time']
data['X4'] = np.random.normal(0, 1, len(data)) + 0.02 * np.cos(data['time'] / 15)
data['X5'] = np.random.gamma(2, 2, len(data)) + 0.04 * data['time']
data['X6'] = np.random.beta(2, 5, len(data)) + 0.01 * np.sin(data['time'] / 20)
data['X7'] = np.random.chisquare(3, len(data)) + 0.03 * data['time']

# 非線形時間トレンドと季節性の生成
nonlinear_trend = 0.1 * time + 0.001 * time**2
seasonality = 2 * np.sin(2 * np.pi * time / 52) + np.sin(2 * np.pi * time / 12)

# アウトカム変数の生成
data['Y'] = (50 +
             np.random.normal(0, 0.5, n_units)[data['unit'] - 1] +  # ユニット固有効果
             nonlinear_trend[data['time']] +  # 非線形時間トレンド
             np.tile(seasonality, n_units) +  # 季節性
             0.5 * data['X1'] +
             0.3 * data['X2'] +
             0.2 * data['X3'] +
             0.4 * data['X4'] +
             0.3 * data['X5'] +
             0.2 * data['X6'] +
             0.1 * data['X7'] +
             np.random.normal(0, 0.5, len(data)))  # ランダムノイズ

# 真の処置効果を計算する関数
def true_treatment_effect(t, treatment_time):
    return 5 * (1 - np.exp(-(t - treatment_time) / 30)) if t >= treatment_time else 0

# 処置効果を追加（最初のn_treated個のユニットのみ）
treatment_effect = np.array([true_treatment_effect(t, treatment_time) for t in data['time']])
data.loc[(data['unit'] <= n_treated) & (data['time'] >= treatment_time), 'Y'] += treatment_effect[(data['unit'] <= n_treated) & (data['time'] >= treatment_time)]

# 予測変数の設定
predictors = ['X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7']

# 1. 合成コントロール法
def synthetic_control(df):
    # 処置前のデータを使用
    pre_treatment = df[df['time'] < treatment_time]
    
    # 処置群と対照群に分割
    treated_units = pre_treatment[pre_treatment['unit'] <= n_treated]
    control_units = pre_treatment[pre_treatment['unit'] > n_treated]
    
    # 予測変数の平均を計算
    X_treated = treated_units.groupby('unit')[predictors].mean()
    X_control = control_units.groupby('unit')[predictors].mean()
    
    # 処置前期間の結果変数
    Y_treated = treated_units.pivot(index='time', columns='unit', values='Y')
    Y_control = control_units.pivot(index='time', columns='unit', values='Y')
    
    # 合成コントロールの重みを最適化する関数
    def get_w(X, X1, Y, Y1):
        def loss(w):
            return np.sqrt(np.mean((Y1 - Y.dot(w))**2))
        
        cons = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1},)
        bounds = [(0, 1) for _ in range(X.shape[0])]
        w0 = np.ones(X.shape[0]) / X.shape[0]
        
        res = minimize(loss, w0, method='SLSQP', constraints=cons, bounds=bounds)
        return res.x
    
    # 各処置ユニットに対して合成コントロールを作成
    treatment_effects = []
    for treated_unit in range(1, n_treated + 1):
        w = get_w(X_control, X_treated.loc[treated_unit], Y_control, Y_treated[treated_unit])
        Y_synthetic = df[df['unit'] > n_treated].pivot(index='time', columns='unit', values='Y').dot(w)
        Y_treated_all = df[df['unit'] == treated_unit].set_index('time')['Y']
        effect = np.mean(Y_treated_all[treatment_time:] - Y_synthetic[treatment_time:])
        treatment_effects.append(effect)
        
        # 時系列グラフの描画
        plt.figure(figsize=(12, 6))
        plt.plot(Y_treated_all.index, Y_treated_all, label='Treated', color='blue')
        plt.plot(Y_synthetic.index, Y_synthetic, label='Synthetic Control', color='red')
        plt.plot(Y_treated_all.index, Y_treated_all - np.array([true_treatment_effect(t, treatment_time) for t in Y_treated_all.index]),
                 label='Treated (Counterfactual)', color='blue', linestyle='--')
        plt.axvline(x=treatment_time, color='green', linestyle='--', label='Treatment Time')
        plt.xlabel('Time')
        plt.ylabel('Outcome')
        plt.legend()
        plt.title(f'Synthetic Control Method - Unit {treated_unit}')
        plt.show()
    
    return np.mean(treatment_effects)


def causal_impact_tf(df):
    # 処置群（最初のn_treated個のユニット）の平均を計算
    treated = df[df['unit'] <= n_treated].groupby('time')['Y'].mean()
    
    # 対照群（残りのユニット）のデータを準備
    control = df[df['unit'] > n_treated].groupby('time')[predictors + ['Y']].mean()
    
    # 処置群と対照群のデータを結合
    data = pd.concat([treated, control], axis=1)
    data.columns = ['y'] + predictors + ['x_avg']
    
    # インデックスを日付型に変更
    start_date = pd.Timestamp('2020-01-01')
    data.index = pd.date_range(start=start_date, periods=len(data), freq='D')
    
    # 処置前後の期間を定義（日付型で）
    pre_period = [start_date, start_date + pd.Timedelta(days=treatment_time-1)]
    post_period = [start_date + pd.Timedelta(days=treatment_time), start_date + pd.Timedelta(days=n_time-1)]
    
    try:
        # Causal Impactモデルの実行
        ci = CausalImpact(data, pre_period, post_period)
        
        # 結果のプロット
        ci.plot()
        plt.show()
        
        # サマリーの表示
        print(ci.summary())
        
        # 処置効果の推定値を返す
        summary = ci.summary_data
        effect = summary.loc['abs_effect', 'average']
        return effect
    except Exception as e:
        print(f"Error in CausalImpact: {e}")
        return np.nan

# 3. 傾向スコアを用いたDID
def propensity_score_did(df):
    def calc_propensity_scores(df):
        X = df.groupby('unit')[predictors].mean().reset_index()
        y = df.groupby('unit')['unit'].first() <= n_treated
        
        clf = LogisticRegression(solver='lbfgs', max_iter=1000)
        clf.fit(X[predictors], y)
        
        return clf.predict_proba(X[predictors])[:, 1]
    
    ps = calc_propensity_scores(df)
    df = df.merge(pd.DataFrame({'unit': df['unit'].unique(), 'ps': ps}), on='unit')
    
    df['weight'] = np.where(df['unit'] <= n_treated, 1 / df['ps'], 1 / (1 - df['ps']))
    df['post'] = (df['time'] >= treatment_time).astype(int)
    df['treated'] = (df['unit'] <= n_treated).astype(int)
    
    model = wls('Y ~ treated + post + treated:post + ' + '+'.join(predictors), data=df, weights=df['weight'])
    results = model.fit()
    
    # 処置前後の平均値を計算
    pre_treat = df[(df['unit'] <= n_treated) & (df['time'] < treatment_time)]['Y'].mean()
    post_treat = df[(df['unit'] <= n_treated) & (df['time'] >= treatment_time)]['Y'].mean()
    pre_control = df[(df['unit'] > n_treated) & (df['time'] < treatment_time)]['Y'].mean()
    post_control = df[(df['unit'] > n_treated) & (df['time'] >= treatment_time)]['Y'].mean()
    
    # 平均値のグラフを描画
    plt.figure(figsize=(10, 6))
    plt.plot([0, 1], [pre_treat, post_treat], 'b-', label='Treated')
    plt.plot([0, 1], [pre_control, post_control], 'r-', label='Control')
    plt.xticks([0, 1], ['Pre-treatment', 'Post-treatment'])
    plt.ylabel('Average Outcome')
    plt.title('DID: Average Outcomes Before and After Treatment')
    plt.legend()
    plt.show()
    
    return results.params['treated:post']

# 各手法での処置効果の推定
print("Estimating synthetic control effect...")
synthetic_effect = synthetic_control(data)
print("Estimating causal impact effect using tfcausalimpact...")
causal_impact_effect = causal_impact_tf(data)
print("Estimating propensity score DID effect...")
ps_did_effect = propensity_score_did(data)

# 真の処置効果の計算
true_effect = np.mean([true_treatment_effect(t, treatment_time) for t in range(treatment_time, n_time)])

# 結果の出力
print(f"真の平均処置効果: {true_effect:.4f}")
print(f"合成コントロール法による推定: {synthetic_effect:.4f}")
print(f"CausalImpactによる推定: {causal_impact_effect:.4f}")
print(f"傾向スコアを用いたDIDによる推定: {ps_did_effect:.4f}")

# 結果の可視化
methods = ['True Effect', 'Synthetic Control', 'CausalImpact', 'PS-DID']
effects = [true_effect, synthetic_effect, causal_impact_effect, ps_did_effect]

plt.figure(figsize=(10, 6))
plt.bar(methods, effects)
plt.title('Comparison of Treatment Effect Estimates')
plt.ylabel('Estimated Effect')
plt.axhline(y=true_effect, color='r', linestyle='--', label='True Effect')
plt.legend()
plt.show()

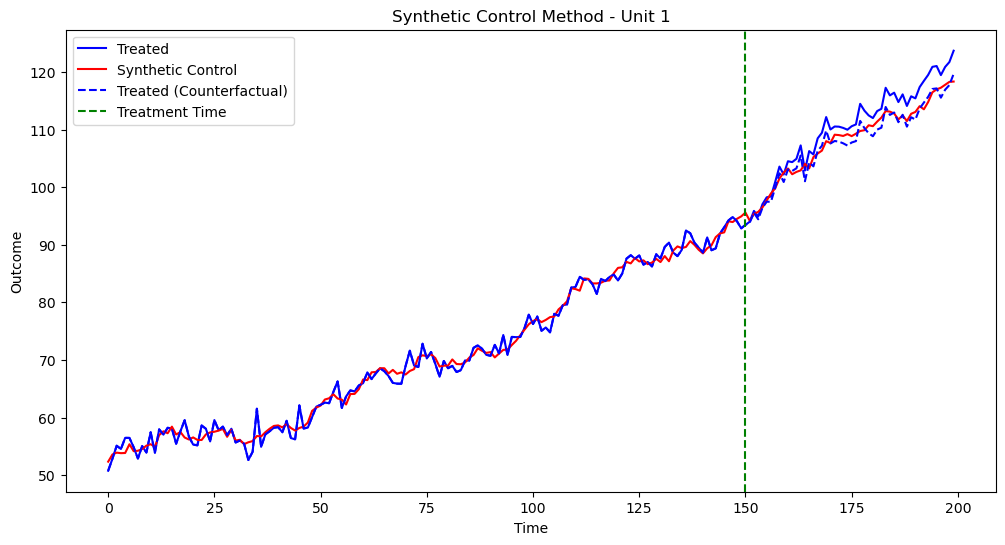
実行結果は以下です Causal Impactの推定結果があまりですね
サンプルデータを複雑にしてみましょう
実行結果は以下です

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from sklearn.linear_model import LogisticRegression
from statsmodels.formula.api import wls
from causalimpact import CausalImpact
from datetime import datetime, timedelta

# ランダムシードを設定（再現性のため）
np.random.seed(42)

# パラメータ設定
n_units = 50  # 総単位数
n_treated = 5  # 処置を受ける単位数
n_time = 300  # 時点数
treatment_time = 200  # 処置が開始される時点

# 時間変数の生成
time = np.arange(n_time)

# データフレームの作成
data = pd.DataFrame({
    'unit': np.repeat(range(1, n_units + 1), n_time),
    'time': np.tile(time, n_units)
})

# 非線形時間トレンドの生成
nonlinear_trend = 10 * np.sin(time / 30) + time / 20

# 季節性の生成
seasonality = 5 * np.sin(2 * np.pi * time / 52)

# ユニット固有の効果を生成
unit_effects = np.random.normal(0, 5, n_units)

# 共変量の生成
data['X1'] = np.random.normal(0, 1, len(data)) + data['unit'] * 0.1
data['X2'] = np.random.uniform(0, 1, len(data)) + np.sin(data['time'] / 10)
data['X3'] = np.random.poisson(5, len(data)) + data['unit'] * 0.2
data['X4'] = np.random.choice(['A', 'B', 'C'], len(data))
data['X5'] = np.random.normal(0, 1, len(data)) + np.cos(data['time'] / 15)
data['X6'] = np.random.gamma(2, 2, len(data)) + data['unit'] * 0.1
data['X7'] = np.random.beta(2, 5, len(data)) + np.sin(data['time'] / 20)
data['X8'] = np.random.chisquare(3, len(data)) + data['time'] * 0.01

# X4のダミー変数を作成
X4_dummies = pd.get_dummies(data['X4'], prefix='X4')
data = pd.concat([data, X4_dummies], axis=1)

# アウトカム変数の生成
data['Y'] = (50 +  # ベースライン
             unit_effects[data['unit'] - 1] +  # ユニット固有効果
             nonlinear_trend[data['time']] +  # 非線形時間トレンド
             seasonality[data['time']] +  # 季節性
             2 * data['X1'] +
             3 * data['X2'] +
             0.5 * data['X3'] +
             1 * data['X4_A'] +
             2 * data['X4_B'] +
             1.5 * data['X5'] +
             0.8 * data['X6'] +
             2.5 * data['X7'] +
             0.3 * data['X8'] +
             np.random.normal(0, 2, len(data)))  # ランダムノイズ

# 時間依存の処置効果を計算する関数
def treatment_effect(t, treatment_time):
    if t < treatment_time:
        return 0
    else:
        return 10 * (1 - np.exp(-(t - treatment_time) / 30))

# 処置効果を追加（最初のn_treated個のユニットのみ）
for t in range(n_time):
    effect = treatment_effect(t, treatment_time)
    data.loc[(data['unit'] <= n_treated) & (data['time'] == t), 'Y'] += effect

# 予測変数の設定
predictors = ['X1', 'X2', 'X3', 'X4_A', 'X4_B', 'X5', 'X6', 'X7', 'X8']

# データの可視化
plt.figure(figsize=(12, 6))
for unit in range(1, 6):  # 最初の5ユニットをプロット
    unit_data = data[data['unit'] == unit]
    plt.plot(unit_data['time'], unit_data['Y'], label=f'Unit {unit}')
plt.axvline(x=treatment_time, color='r', linestyle='--', label='Treatment Time')
plt.xlabel('Time')
plt.ylabel('Outcome')
plt.legend()
plt.title('Sample Data Visualization')
plt.show()

# 1. 合成コントロール法
def synthetic_control(df):
    # 処置前のデータを使用
    pre_treatment = df[df['time'] < treatment_time]
    
    # 処置群と対照群に分割
    treated_units = pre_treatment[pre_treatment['unit'] <= n_treated]
    control_units = pre_treatment[pre_treatment['unit'] > n_treated]
    
    # 予測変数の平均を計算
    X_treated = treated_units.groupby('unit')[predictors].mean()
    X_control = control_units.groupby('unit')[predictors].mean()
    
    # 処置前期間の結果変数
    Y_treated = treated_units.pivot(index='time', columns='unit', values='Y')
    Y_control = control_units.pivot(index='time', columns='unit', values='Y')
    
    # 合成コントロールの重みを最適化する関数
    def get_w(X, X1, Y, Y1):
        def loss(w):
            return np.sqrt(np.mean((Y1 - Y.dot(w))**2))
        
        cons = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1},)
        bounds = [(0, 1) for _ in range(X.shape[0])]
        w0 = np.ones(X.shape[0]) / X.shape[0]
        
        res = minimize(loss, w0, method='SLSQP', constraints=cons, bounds=bounds)
        return res.x
    
    # 各処置ユニットに対して合成コントロールを作成
    treatment_effects = []
    for treated_unit in range(1, n_treated + 1):
        w = get_w(X_control, X_treated.loc[treated_unit], Y_control, Y_treated[treated_unit])
        Y_synthetic = df[df['unit'] > n_treated].pivot(index='time', columns='unit', values='Y').dot(w)
        Y_treated_all = df[df['unit'] == treated_unit].set_index('time')['Y']
        effect = np.mean(Y_treated_all[treatment_time:] - Y_synthetic[treatment_time:])
        treatment_effects.append(effect)
        
        # 時系列グラフの描画
        plt.figure(figsize=(12, 6))
        plt.plot(Y_treated_all.index, Y_treated_all, label='Treated', color='blue')
        plt.plot(Y_synthetic.index, Y_synthetic, label='Synthetic Control', color='red')
        plt.plot(Y_treated_all.index, Y_treated_all - np.array([true_treatment_effect(t, treatment_time) for t in Y_treated_all.index]),
                 label='Treated (Counterfactual)', color='blue', linestyle='--')
        plt.axvline(x=treatment_time, color='green', linestyle='--', label='Treatment Time')
        plt.xlabel('Time')
        plt.ylabel('Outcome')
        plt.legend()
        plt.title(f'Synthetic Control Method - Unit {treated_unit}')
        plt.show()
    
    return np.mean(treatment_effects)

def causal_impact_tf(df):
    # 処置群（最初のn_treated個のユニット）の平均を計算
    treated = df[df['unit'] <= n_treated].groupby('time')['Y'].mean()
    
    # 対照群（残りのユニット）のデータを準備
    control = df[df['unit'] > n_treated].groupby('time')[predictors + ['Y']].mean()
    
    # 処置群と対照群のデータを結合
    data = pd.concat([treated, control], axis=1)
    data.columns = ['y'] + predictors + ['x_avg']
    
    # インデックスを日付型に変更
    start_date = pd.Timestamp('2020-01-01')
    data.index = pd.date_range(start=start_date, periods=len(data), freq='D')
    
    # 処置前後の期間を定義（日付型で）
    pre_period = [start_date, start_date + pd.Timedelta(days=treatment_time-1)]
    post_period = [start_date + pd.Timedelta(days=treatment_time), start_date + pd.Timedelta(days=n_time-1)]
    
    try:
        # Causal Impactモデルの実行
        ci = CausalImpact(data, pre_period, post_period)
        
        # 結果のプロット
        ci.plot()
        plt.show()
        
        # サマリーの表示
        print(ci.summary())
        
        # 処置効果の推定値を返す
        summary = ci.summary_data
        effect = summary.loc['abs_effect', 'average']
        return effect
    except Exception as e:
        print(f"Error in CausalImpact: {e}")
        return np.nan

# 3. 傾向スコアを用いたDID
def propensity_score_did(df):
    def calc_propensity_scores(df):
        X = df.groupby('unit')[predictors].mean().reset_index()
        y = df.groupby('unit')['unit'].first() <= n_treated
        
        clf = LogisticRegression(solver='lbfgs', max_iter=1000)
        clf.fit(X[predictors], y)
        
        return clf.predict_proba(X[predictors])[:, 1]
    
    ps = calc_propensity_scores(df)
    df = df.merge(pd.DataFrame({'unit': df['unit'].unique(), 'ps': ps}), on='unit')
    
    df['weight'] = np.where(df['unit'] <= n_treated, 1 / df['ps'], 1 / (1 - df['ps']))
    df['post'] = (df['time'] >= treatment_time).astype(int)
    df['treated'] = (df['unit'] <= n_treated).astype(int)
    
    model = wls('Y ~ treated + post + treated:post + ' + '+'.join(predictors), data=df, weights=df['weight'])
    results = model.fit()
    
    # 処置前後の平均値を計算
    pre_treat = df[(df['unit'] <= n_treated) & (df['time'] < treatment_time)]['Y'].mean()
    post_treat = df[(df['unit'] <= n_treated) & (df['time'] >= treatment_time)]['Y'].mean()
    pre_control = df[(df['unit'] > n_treated) & (df['time'] < treatment_time)]['Y'].mean()
    post_control = df[(df['unit'] > n_treated) & (df['time'] >= treatment_time)]['Y'].mean()
    
    # 平均値のグラフを描画
    plt.figure(figsize=(10, 6))
    plt.plot([0, 1], [pre_treat, post_treat], 'b-', label='Treated')
    plt.plot([0, 1], [pre_control, post_control], 'r-', label='Control')
    plt.xticks([0, 1], ['Pre-treatment', 'Post-treatment'])
    plt.ylabel('Average Outcome')
    plt.title('DID: Average Outcomes Before and After Treatment')
    plt.legend()
    plt.show()
    
    return results.params['treated:post']

# 各手法での処置効果の推定
print("Estimating synthetic control effect...")
synthetic_effect = synthetic_control(data)
print("Estimating causal impact effect using tfcausalimpact...")
causal_impact_effect = causal_impact_tf(data)
print("Estimating propensity score DID effect...")
ps_did_effect = propensity_score_did(data)

# 真の処置効果の計算
true_effect = np.mean([true_treatment_effect(t, treatment_time) for t in range(treatment_time, n_time)])

# 結果の出力
print(f"真の平均処置効果: {true_effect:.4f}")
print(f"合成コントロール法による推定: {synthetic_effect:.4f}")
print(f"CausalImpactによる推定: {causal_impact_effect:.4f}")
print(f"傾向スコアを用いたDIDによる推定: {ps_did_effect:.4f}")

# 結果の可視化
methods = ['True Effect', 'Synthetic Control', 'CausalImpact', 'PS-DID']
effects = [true_effect, synthetic_effect, causal_impact_effect, ps_did_effect]

plt.figure(figsize=(10, 6))
plt.bar(methods, effects)
plt.title('Comparison of Treatment Effect Estimates')
plt.ylabel('Estimated Effect')
plt.axhline(y=true_effect, color='r', linestyle='--', label='True Effect')
plt.legend()
plt.show()

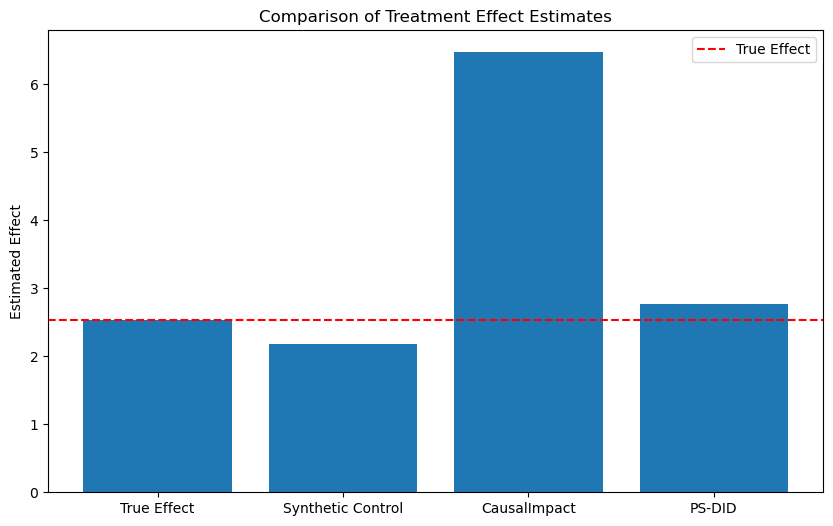
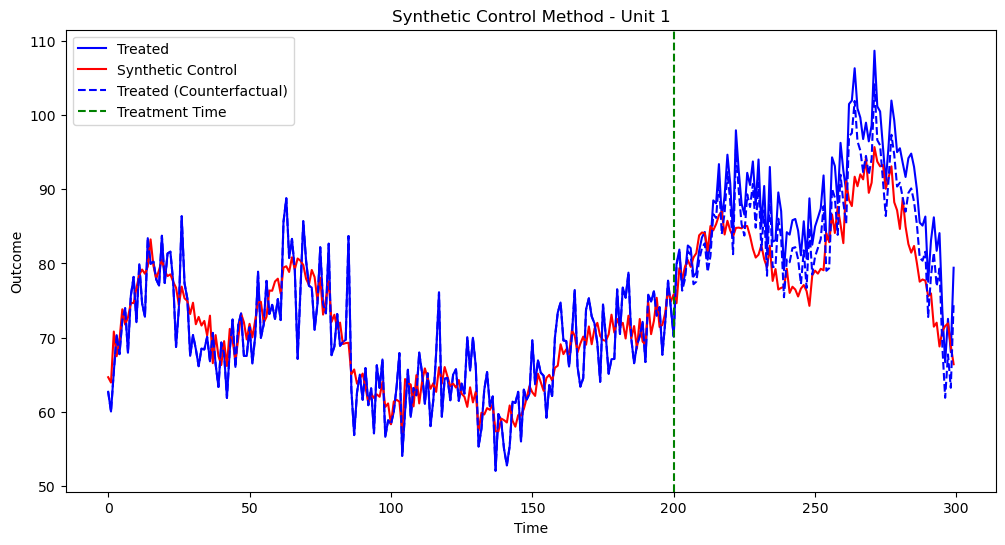
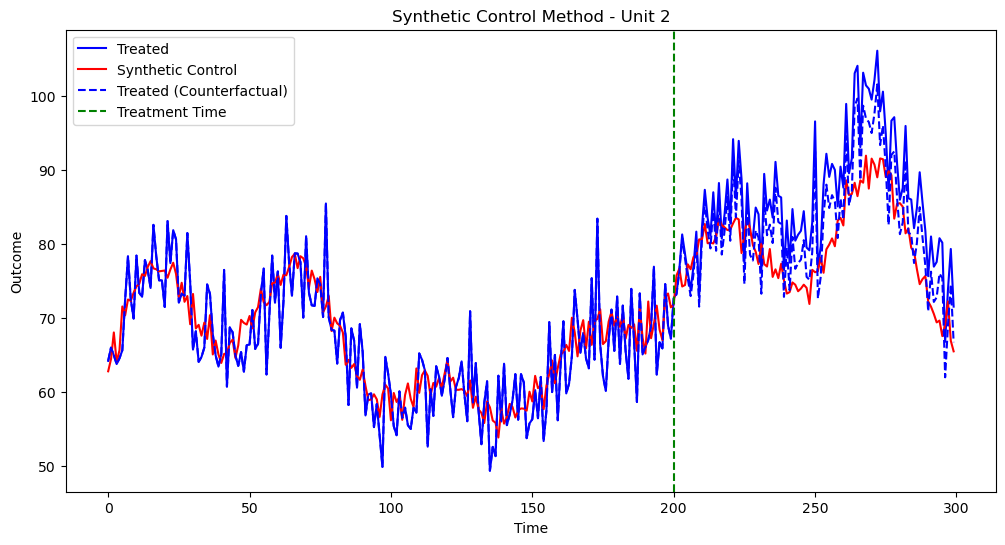
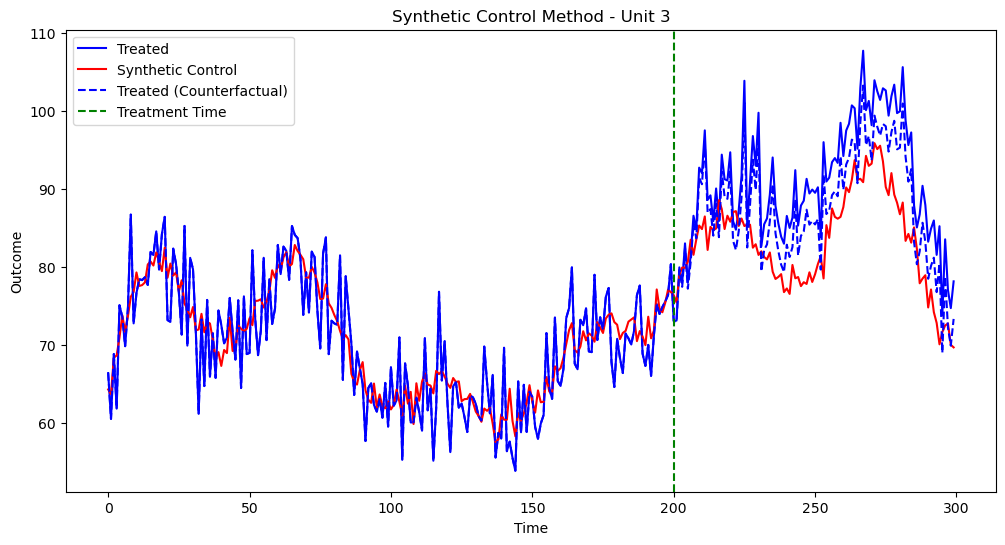
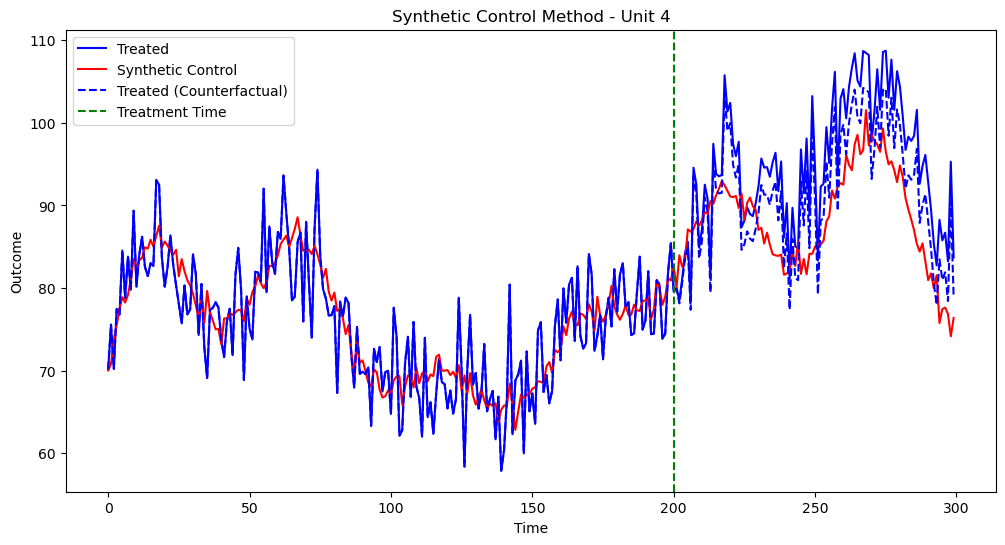
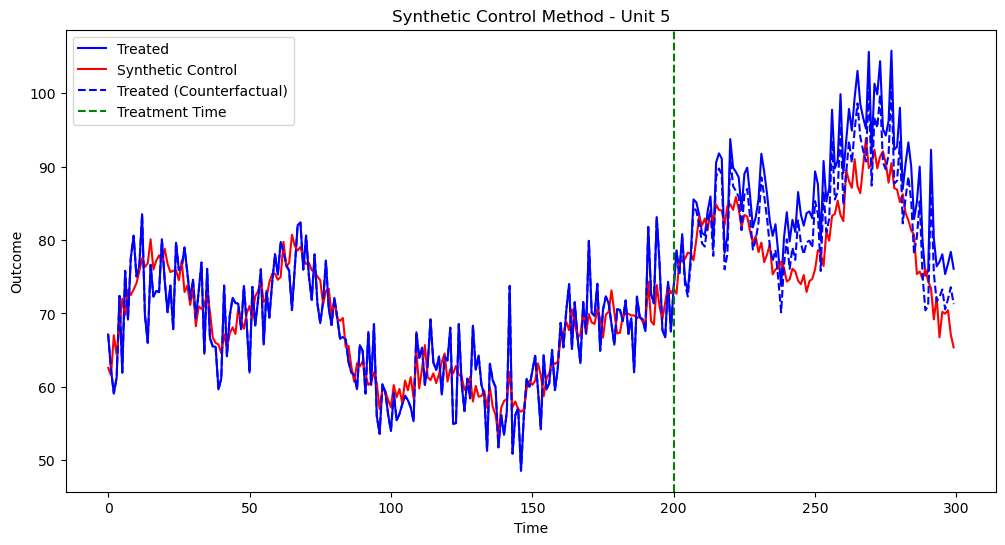
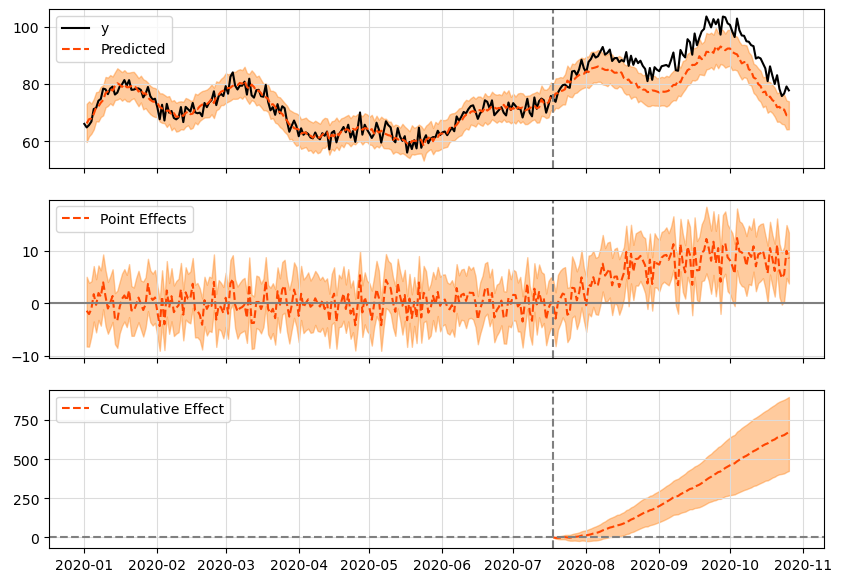
実行結果は以下です 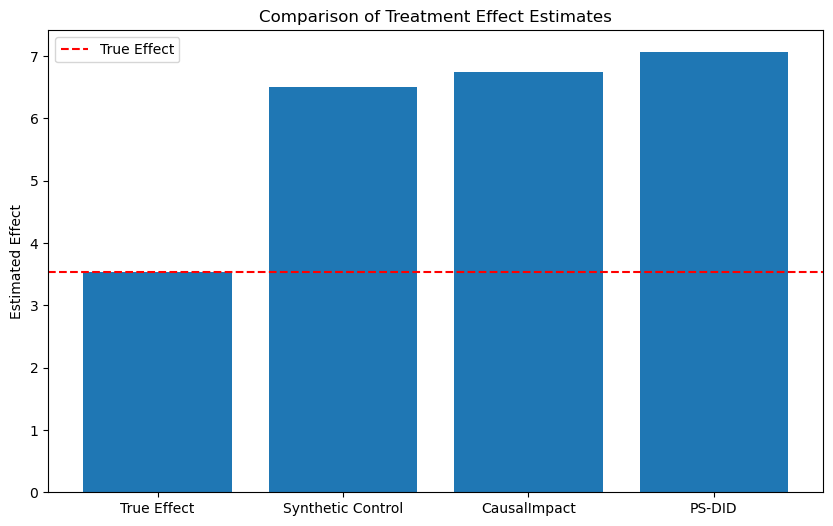サンプルデータが複雑になると、脱落変数のバイアスとかが無くても、推定精度が下がるんですね...

最後に

今回は、合成コントロール法に関して取り上げてみましたが、どうだったでしょうか？まあ主体は付録の方なんですけどね...
個人的に付録の結果はとても意外でした。CausalImpactに関しては、コードを回すたびに推定のブレが大きく難しいなと感じた次第です。
今回のサンプルデータは、Claude3に考えてもらったので私はノータッチです。ここまでのサンプルデータは私には考えられないです（笑）
参考になれば幸いです。