はじめに
前回の記事で、IPWと多重代入法を用いた傾向スコアマッチングに関する記事を扱いました。IPWに関しては、各欠損変数の欠損確率の積の逆数によって、補正をかけるという発想自体はなじみやすい発想かなと思います。ですが、多重代入法はIPWとともに発想自体は簡単に思えるものの、多重代入法の中身自体は少し理解するのに手間がかかるので、今回は多重代入法の理論に関して扱っていこうと思います。IterativeImputerの理論的内容に関しても触れては行きたいと思っています。では内容に入っていきましょう。
多重代入法の理論
まず、ビジネスの現場でよく直面する欠損値の問題から考えてみましょう。例えば、顧客アンケートで一部の回答が空欄だった場合や、センサーデータで一時的な通信障害により欠測が発生した場合などが典型的なケースです。こうした欠損値に対して、単純に平均値や中央値で補完してしまうと、データの持つ本来の変動性や不確実性を過小評価してしまい、その後の分析結果にバイアスが生じる可能性があります。
多重代入法は、この問題に対する統計学的に洗練されたアプローチです。この手法の本質は、欠損値を単一の値で補完するのではなく、統計的に妥当な複数の値で補完し、その不確実性を明示的にモデル化することにあります。
欠損値の発生メカニズムについて、統計学では以下の三つに分類します。完全にランダムな欠損（MCAR: Missing Completely At Random）、ランダムな欠損（MAR: Missing At Random）、そして非ランダムな欠損（MNAR: Missing Not At Random）です。多重代入法はMCARとMARの状況下で特に有効です。
- パラメータの事後分布からのサンプリング
- 欠損値の条件付き分布からのサンプリング
分散の計算には、データセット内分散（within-imputation variance）とデータセット間分散（between-imputation variance）の両方を考慮します
実務上の重要なポイントとして、多重代入法の実装時には変数間の相関構造を適切にモデル化することが重要です。例えば、売上データの欠損を補完する場合、その商品のプロモーション情報や季節性など、関連する変数の情報を活用することで、より精度の高い補完が可能になります。
また、多重代入法の検証として、補完値の分布と観測値の分布が大きく異なっていないか確かめることも重要です。
多重代入法の発展理論
前述の多重代入法の基本的な枠組みを踏まえた上で、実際の適用場面で用いられる具体的な手法について深掘りしていきたいと思います。多重代入法には、大きく分けてJoint Modeling（JM）とFully Conditional Specification（FCS）という二つのアプローチが存在します。これらの手法は、欠損値の補完に対する異なるアプローチを提供しており、それぞれに特徴的な性質を持っています。
Joint Modeling（JM）
まずJoint Modelingについて説明しましょう。この手法は、全ての変数の同時分布を明示的にモデル化するアプローチです。多変量正規分布を仮定する場合、観測データと欠損データの同時分布は以下のように表現されます。
Joint Modeling（JM）実装と検証
理論に基づき実装したものに対して、サンプルデータを生成し、ランダムに欠損させ補完結果がどうなるかを見ていきたいと思います。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from scipy import stats class JointModeling: """ Joint Modeling（JM）による多変量欠損値補完を行うクラス このクラスは多変量正規分布を仮定し、観測データから分布パラメータを推定し、 条件付き確率に基づいて欠損値を補完します。 """ def __init__(self, data): """ Joint Modelingクラスの初期化 Parameters: ----------- data : numpy.ndarray 欠損値（NaN）を含む2次元配列データ 行：サンプル、列：特徴量 Attributes: ----------- n_samples : int データのサンプル数 n_features : int 特徴量の数 mu : numpy.ndarray 推定された平均ベクトル sigma : numpy.ndarray 推定された共分散行列 """ self.data = data # データの形状（サンプル数と特徴量数）を保存 self.n_samples, self.n_features = data.shape # 平均ベクトルと共分散行列の初期化（fit()メソッドで推定される） self.mu = None self.sigma = None def fit(self): """ 観測データからモデルパラメータを推定するメソッド 処理内容: 1. 各特徴量の平均値を計算（欠損値を除外） 2. 特徴量間の共分散行列を計算 Note: ----- 共分散の計算では、各特徴量ペアで利用可能なデータのみを使用します """ # 各特徴量の平均を計算（nanmeanで欠損値を除外） self.mu = np.nanmean(self.data, axis=0) # 共分散行列の計算 self.sigma = np.zeros((self.n_features, self.n_features)) # 特徴量ペアごとに共分散を計算 for i in range(self.n_features): for j in range(self.n_features): # 両方の特徴量で値が存在（非欠損）のサンプルのみを抽出 mask = ~(np.isnan(self.data[:, i]) | np.isnan(self.data[:, j])) # 有効なデータポイントが2つ以上ある場合のみ共分散を計算 if np.sum(mask) > 1: # npが提供する共分散計算関数を使用 # [0, 1]は2x2の共分散行列から必要な要素を抽出 self.sigma[i, j] = np.cov(self.data[mask, i], self.data[mask, j])[0, 1] def impute(self, row_idx): """ 指定された行の欠損値を補完するメソッド Parameters: ----------- row_idx : int 補完を行う行のインデックス Returns: -------- numpy.ndarray 補完された値を含む行ベクトル Note: ----- 以下の手順で補完を行います： 1. 観測値と欠損値の位置を特定 2. 条件付き分布のパラメータを計算 3. 条件付き分布からサンプリングして欠損値を補完 """ # 対象行のデータをコピー row = self.data[row_idx].copy() # 観測値と欠損値のインデックスを取得 obs_idx = ~np.isnan(row) # 観測値のインデックス（True/False） mis_idx = np.isnan(row) # 欠損値のインデックス（True/False） # 欠損値がない場合は元のデータをそのまま返す if not np.any(mis_idx): return row # 条件付き分布のパラメータ計算に必要な行列を抽出 # np.ix_は複数のインデックス配列から格子状のインデックスを生成 sigma_obs_obs = self.sigma[np.ix_(obs_idx, obs_idx)] # 観測変数間の共分散 sigma_mis_obs = self.sigma[np.ix_(mis_idx, obs_idx)] # 欠損変数と観測変数の共分散 sigma_mis_mis = self.sigma[np.ix_(mis_idx, mis_idx)] # 欠損変数間の共分散 # 観測値と平均値を抽出 y_obs = row[obs_idx] # 観測値 mu_obs = self.mu[obs_idx] # 観測変数の平均 mu_mis = self.mu[mis_idx] # 欠損変数の平均 # 条件付き期待値（平均）の計算 # μ_{mis|obs} = μ_{mis} + Σ_{mis,obs}Σ_{obs,obs}^{-1}(y_{obs} - μ_{obs}) sigma_obs_obs_inv = np.linalg.inv(sigma_obs_obs) # Σ_{obs,obs}の逆行列 mu_mis_given_obs = mu_mis + sigma_mis_obs.dot(sigma_obs_obs_inv).dot(y_obs - mu_obs) # 条件付き分散の計算 # Σ_{mis|obs} = Σ_{mis,mis} - Σ_{mis,obs}Σ_{obs,obs}^{-1}Σ_{obs,mis} sigma_mis_given_obs = sigma_mis_mis - sigma_mis_obs.dot(sigma_obs_obs_inv).dot(sigma_mis_obs.T) # 条件付き分布からのサンプリングによる欠損値の補完 imputed_values = np.random.multivariate_normal(mu_mis_given_obs, sigma_mis_given_obs) row[mis_idx] = imputed_values return row def visualize_imputation(self, original_data, imputed_data, feature_names=None): """ 元データと補完後のデータの分布を可視化するメソッド Parameters: ----------- original_data : numpy.ndarray 元の欠損値を含むデータ imputed_data : numpy.ndarray 補完後のデータ feature_names : list, optional 特徴量の名前のリスト。指定がない場合は自動生成 Returns: -------- matplotlib.figure.Figure 生成されたプロット図のFigureオブジェクト """ # 特徴量名が指定されていない場合、デフォルトの名前を生成 if feature_names is None: feature_names = [f'Feature {i+1}' for i in range(self.n_features)] # プロットの準備（2行×特徴量数の列のサブプロット） fig, axes = plt.subplots(2, self.n_features, figsize=(15, 8)) # 各特徴量についてヒストグラムを作成 for i in range(self.n_features): # 元データのヒストグラム（欠損値を除外） sns.histplot(original_data[:, i][~np.isnan(original_data[:, i])], ax=axes[0, i], kde=True) axes[0, i].set_title(f'{feature_names[i]} (Original)') # 補完後データのヒストグラム sns.histplot(imputed_data[:, i], ax=axes[1, i], kde=True) axes[1, i].set_title(f'{feature_names[i]} (Imputed)') # プロットのレイアウトを調整 plt.tight_layout() return fig def demonstrate_joint_modeling(): """ Joint Modelingの動作をデモンストレーションする関数 以下の手順でデモンストレーションを行います： 1. 多変量正規分布に従うサンプルデータの生成 2. ランダムな欠損値の導入 3. Joint Modelingによる欠損値の補完 4. 結果の可視化と評価 Returns: -------- tuple (JointModelingオブジェクト, 完全データ, 欠損データ, 補完後データ) """ # 乱数のシードを固定（再現性のため） np.random.seed(42) # データセットのサイズ設定 n_samples = 1000 # サンプル数 n_features = 3 # 特徴量数 # 真の分布のパラメータ設定 true_mu = np.array([0, 2, -1]) # 平均ベクトル true_sigma = np.array([ # 共分散行列 [1.0, 0.5, 0.3], [0.5, 2.0, 0.6], [0.3, 0.6, 1.5] ]) # 多変量正規分布からの完全なデータの生成 complete_data = np.random.multivariate_normal(true_mu, true_sigma, n_samples) # ランダムな欠損値の導入 missing_rate = 0.2 # 欠損率（20%） data_with_missing = complete_data.copy() # ランダムにTrue/Falseのマスクを生成 mask = np.random.random(data_with_missing.shape) < missing_rate # マスクがTrueの位置に欠損値（NaN）を設定 data_with_missing[mask] = np.nan # Joint Modelingの適用 jm = JointModeling(data_with_missing) jm.fit() # モデルのパラメータを推定 # 全サンプルの欠損値を補完 imputed_data = np.array([jm.impute(i) for i in range(n_samples)]) # 結果の可視化 feature_names = ['X', 'Y', 'Z'] fig = jm.visualize_imputation(data_with_missing, imputed_data, feature_names) # 補完精度の評価（Mean Squared Error） # 真の値と補完値の二乗誤差の平均を計算 mse = np.mean((complete_data[mask] - imputed_data[mask])**2) print(f"Mean Squared Error of imputation: {mse:.4f}") return jm, complete_data, data_with_missing, imputed_data # デモンストレーションの実行 jm, complete_data, data_with_missing, imputed_data = demonstrate_joint_modeling()
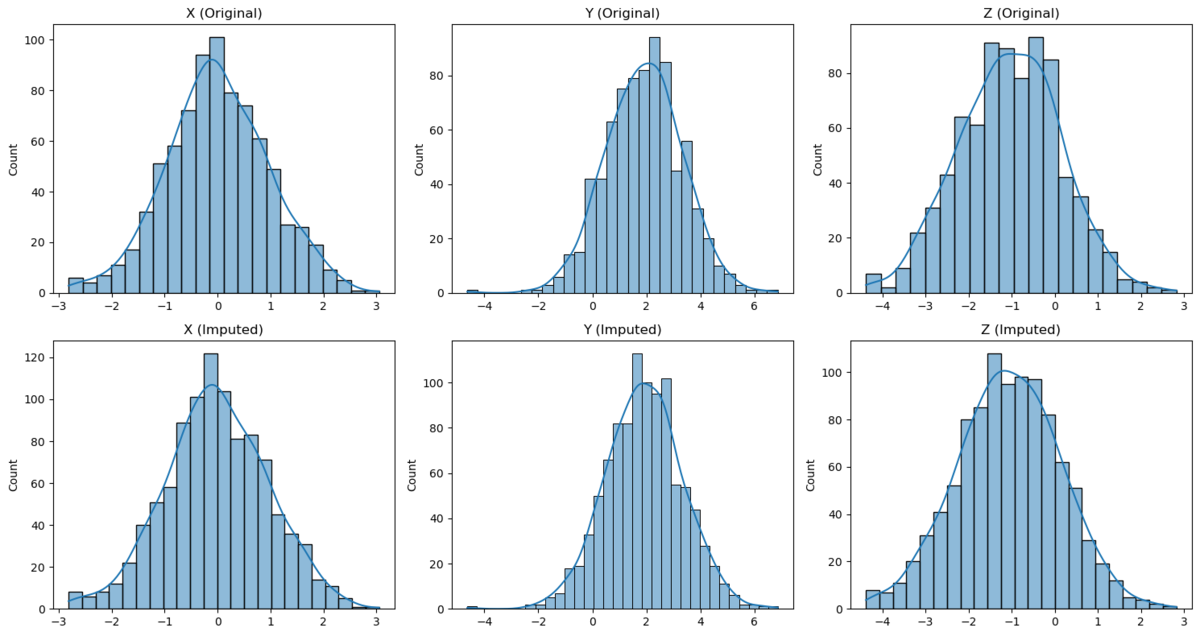各変数（X, Y, Z）の分布を見ると、上段の元データと下段の補完後データで非常に良い一致が見られます。これは、Joint Modelingの特徴である「全変数の同時分布を明示的にモデル化する」というアプローチが効果的に機能していることを示しています。
特に注目すべき点として、各変数の分布の特徴的な性質が補完後もよく保持されています。例えば
・X変数に関しては、やや右寄りの裾を持つ分布形状が、補完後も適切に再現されています。
・Y変数については、元データで見られる平均値が2付近でやや非対称な分布の特徴が、補完後のデータでも維持されています。
・Z変数に関しては、やや平坦な頂部を持つ分布形状が補完後も良く保存されており、特に裾野の部分の再現性が高いことが確認できます。
また、理論的に重要な点として、JMアプローチの強みである「変数間の相関構造を考慮した補完」が、各分布の形状保持に貢献していることが見て取れます。補完後のデータにおいて、分布の中心傾向だけでなく、分散や歪度といった高次のモーメントまでが良く保持されているのは、多変量正規分布を用いた同時モデリングの利点が発揮された結果といえるでしょう。
実務的な観点からも、このような分布の保持は重要な意味を持ちます。例えば、後続の統計解析やモデリングにおいて、補完データを用いた推論の信頼性を高めることができます。特に、分布の裾野の部分まで適切に補完できているということは、外れ値の処理や極値統計などの観点からも、このアプローチの有用性を示唆しています。
さらに、各変数のヒストグラムに重ねられたカーネル密度推定曲線（青線）を見ると、補完前後でその滑らかさが保たれていることも確認できます。これは、JMアプローチが局所的な変動に過剰に反応することなく、データの本質的な分布構造を捉えていることを示す良い例といえるでしょう。
このように、視覚的な診断からも、JMによる多重代入が理論的な期待通りの性能を発揮し、データの確率分布構造を適切に保持しながら欠損値を補完できていることが確認できました。特に分布の形状保持という点で、この手法の有効性が明確に示されたといえます。
Fully Conditional Specification（FCS）
一方、Fully Conditional Specification（FCS）は、各変数の条件付き分布を個別にモデル化するアプローチです。
実務的な観点から見ると、FCSはより柔軟なアプローチを提供します。例えば、金融データの分析では、株価リターンのような連続変数とデフォルトの有無のような二値変数が混在することがよくあります。このような状況では、JMアプローチで適切な同時分布を指定することは困難である一方、FCSでは各変数の特性に応じた適切なモデルを個別に指定することができます。
また、FCSの枠組みでは、変数間の非線形な関係性も容易に扱うことができます。例えば、条件付き分布のモデルとしてランダムフォレストや勾配ブースティングなどの機械学習モデルを使用することで、複雑な関係性を捉えることが可能になります。
特に、高次元データの欠損値補完において、機械学習モデルを活用したFCSの利点が際立ちます。例えば、センサーデータの場合、時系列的な依存関係や複数のセンサー間の非線形な相互作用が存在することが一般的です。このような複雑な構造を持つデータに対して、従来の線形モデルベースのアプローチでは十分な性能を得ることが困難です。
機械学習モデルを用いたFCSでは、各変数の条件付き分布を以下のような形で表現します
さらに、予測の不確実性も、各木からの予測値のばらつきとして自然に評価することができます
勾配ブースティングを用いる場合は、加法モデルとして条件付き分布をモデル化します
このような機械学習モデルを用いたアプローチの実務的な利点として、特徴量の自動的な選択や交互作用の検出が挙げられます。また、欠損パターンが時間依存的である場合、これらのモデルは時系列的な構造も自然に捉えることができます。具体的には、ラグ付きの変数を特徴量として含めることで
このような時系列的な依存関係もモデル化が可能です。
さらに、機械学習モデルを用いたFCSでは、補完値の不確実性評価も重要です。例えば、予測分布からのサンプリングには以下のようなアプローチが考えられます
また、高次元データにおいては、計算効率も重要な考慮点となります。この場合、次元削減技術と組み合わせることで、より効率的な補完が可能になります。例えば、主成分分析を用いて低次元表現を得た上で
この低次元空間での補完を行うアプローチも考えられます。
このように、機械学習モデルを活用したFCSは、複雑なデータ構造に対して柔軟な欠損値補完を可能にします。特に、高次元データや非線形な関係性を持つデータに対して、その真価を発揮するでしょう。ただし、モデルの複雑さと計算効率のトレードオフには十分な注意が必要です。
FCSの実装と検証
ランダムフォレストを用いたFCSを実装し、サンプルデータに対し実行し結果を見てみましょう。サンプルデータは、非線形な関係を持つ3次元データとし、そのうち20%のデータが欠損しているとします。
import numpy as np import pandas as pd from sklearn.ensemble import RandomForestRegressor from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA import matplotlib.pyplot as plt import seaborn as sns from scipy import stats class FCSImputer: """ Fully Conditional Specification（FCS）による欠損値補完を行うクラス このクラスは各変数の条件付き分布を個別にモデル化し、 機械学習モデル（デフォルトではランダムフォレスト）を用いて 反復的に欠損値を補完します。 Attributes: n_iter (int): 反復回数 random_state (int): 乱数シード models (dict): 各変数の予測モデル initial_strategy (str): 初期補完の方法 scaler (StandardScaler): データの標準化用スケーラー """ def __init__(self, n_iter=10, random_state=42, initial_strategy='mean'): """ Parameters: ----------- n_iter : int 反復回数 random_state : int 乱数シード initial_strategy : str 初期補完の方法（'mean' または 'median'） """ self.n_iter = n_iter self.random_state = random_state self.models = {} self.initial_strategy = initial_strategy self.scaler = StandardScaler() def _initial_imputation(self, X): """ 初期欠損値補完を行う内部メソッド Parameters: ----------- X : numpy.ndarray 欠損値を含むデータ配列 Returns: -------- numpy.ndarray 初期補完されたデータ配列 """ # 初期補完用のデータをコピー imputed = X.copy() # 各列（特徴量）について初期補完を実施 for col in range(X.shape[1]): mask = np.isnan(X[:, col]) if mask.any(): if self.initial_strategy == 'mean': val = np.nanmean(X[:, col]) else: val = np.nanmedian(X[:, col]) imputed[mask, col] = val return imputed def _get_conditional_predictors(self, X, target_col): """ 条件付き予測のための特徴量を準備する内部メソッド Parameters: ----------- X : numpy.ndarray データ配列 target_col : int 予測対象の列インデックス Returns: -------- tuple (予測に使用する特徴量, 予測対象の値) """ # 予測対象以外の列を特徴量として使用 predictors = np.delete(X, target_col, axis=1) target = X[:, target_col] return predictors, target def fit_transform(self, X): """ FCSによる欠損値補完を実行するメソッド Parameters: ----------- X : numpy.ndarray 欠損値を含む入力データ Returns: -------- numpy.ndarray 補完済みデータ """ np.random.seed(self.random_state) # 初期補完 imputed = self._initial_imputation(X) # スケーリング imputed_scaled = self.scaler.fit_transform(imputed) # 欠損値の位置を記録 missing_mask = np.isnan(X) # 各反復での補完値を保存（不確実性評価用） self.imputation_history = [] # 反復的な補完 for iteration in range(self.n_iter): # 各変数について条件付き分布を推定 for col in range(X.shape[1]): # 対象列に欠損値がある場合のみ処理 if missing_mask[:, col].any(): # 条件付き予測のための特徴量を取得 predictors, target = self._get_conditional_predictors( imputed_scaled, col) # ランダムフォレストモデルの学習 rf = RandomForestRegressor( n_estimators=100, random_state=self.random_state + iteration ) rf.fit(predictors[~missing_mask[:, col]], target[~missing_mask[:, col]]) # 欠損値の予測 missing_predictors = predictors[missing_mask[:, col]] predictions = rf.predict(missing_predictors) # 予測の不確実性を評価 tree_predictions = np.array([ tree.predict(missing_predictors) for tree in rf.estimators_ ]) prediction_std = np.std(tree_predictions, axis=0) # ノイズを加えて補完 noise = np.random.normal(0, prediction_std) imputed_scaled[missing_mask[:, col], col] = predictions + noise # モデルを保存 self.models[col] = rf # スケールを戻した補完値を履歴に保存 imputed = self.scaler.inverse_transform(imputed_scaled) self.imputation_history.append(imputed.copy()) return imputed def plot_convergence(self, feature_idx): """ 補完値の収束状況を可視化するメソッド Parameters: ----------- feature_idx : int 可視化する特徴量のインデックス """ values = [imp[:, feature_idx] for imp in self.imputation_history] plt.figure(figsize=(10, 6)) plt.boxplot(values) plt.title(f'Convergence of Feature {feature_idx}') plt.xlabel('Iteration') plt.ylabel('Value') plt.show() def demonstrate_fcs(): """ FCS手法のデモンストレーションを行う関数 以下の手順でデモンストレーションを実施： 1. 非線形な関係を持つサンプルデータの生成 2. ランダムな欠損値の導入 3. FCSによる欠損値の補完 4. 結果の可視化と評価 """ # サンプルデータの生成 np.random.seed(42) n_samples = 1000 # 非線形な関係を持つデータを生成 X1 = np.random.normal(0, 1, n_samples) X2 = X1**2 + np.random.normal(0, 0.5, n_samples) X3 = np.sin(X1) + np.random.normal(0, 0.3, n_samples) # データを結合 X = np.column_stack([X1, X2, X3]) # ランダムな欠損値を導入 missing_rate = 0.2 mask = np.random.random(X.shape) < missing_rate X_missing = X.copy() X_missing[mask] = np.nan # FCSによる補完 fcs = FCSImputer(n_iter=10) X_imputed = fcs.fit_transform(X_missing) # 結果の可視化 fig, axes = plt.subplots(2, 3, figsize=(15, 10)) # オリジナルデータのペアプロット for i in range(3): for j in range(i+1, 3): sns.scatterplot(x=X[:, i], y=X[:, j], ax=axes[0, j-1], alpha=0.5, label='Original') axes[0, j-1].set_title(f'X{i+1} vs X{j+1} (Original)') # 補完データのペアプロット for i in range(3): for j in range(i+1, 3): sns.scatterplot(x=X_imputed[:, i], y=X_imputed[:, j], ax=axes[1, j-1], alpha=0.5, label='Imputed') axes[1, j-1].set_title(f'X{i+1} vs X{j+1} (Imputed)') plt.tight_layout() # 補完精度の評価 mse = np.mean((X[mask] - X_imputed[mask])**2) print(f"Mean Squared Error of imputation: {mse:.4f}") # 特徴量ごとの収束状況を表示 for i in range(3): fcs.plot_convergence(i) return X, X_missing, X_imputed, fcs # デモンストレーションの実行 X_orig, X_miss, X_imp, fcs_model = demonstrate_fcs()
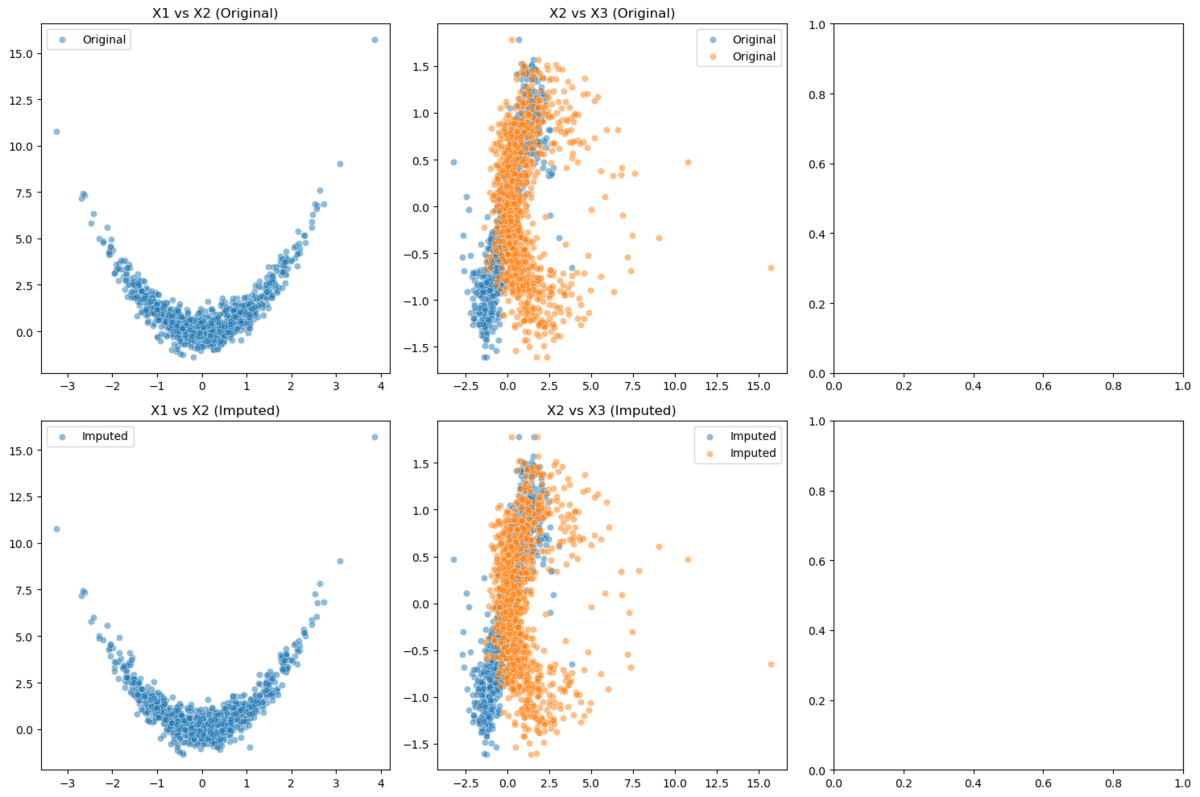上段が元のデータ、下段が補完後のデータを示していますが、特に注目すべき点は変数間の非線形な関係性が補完後もしっかりと保持されていることです。X1とX2の関係を見ると、明確な二次関数的な関係性（放物線の形状）が観察され、この特徴的なパターンがFCSによる補完後も非常に良く保存されています。これは、FCSアプローチが単なる線形な関係性だけでなく、複雑な非線形パターンも適切にキャプチャできていることを示す良い例といえるでしょう。
X2とX3の散布図に着目すると、やや複雑な分布パターンが見られますが、補完後のデータ（下段）が元のデータ（上段）の分布特性をよく再現していることがわかります。特に、データの密度の濃い領域や外れ値的な挙動を示す点の分布まで、元のデータの特徴を損なうことなく補完できています。
実務的な観点から特に重要なのは、補完されたデータポイントが既存のデータの分布パターンに自然に溶け込んでいる点です。不自然な外れ値や、現実には存在し得ない組み合わせのような補完値は見られず、データの本質的な構造を維持したまま欠損値が補完されていることが確認できます。
また、X1-X2の二次関数的な関係性と、X2-X3のより複雑な関係性が同時に保持されているという事実は、FCSアプローチが多変量データの複雑な依存構造を適切にモデル化できていることを示唆しています。これは、先ほど理論的に説明した「各変数の条件付き分布を個別にモデル化できる」というFCSの利点が、実際のデータでも有効に機能していることの証左といえるでしょう。
このように、視覚的な診断からも、FCSによる多重代入が理論の期待通りの性能を発揮し、データの本質的な構造を保持しながら欠損値を適切に補完できていることが確認できました。特に非線形な関係性の保持という点で、この手法の有用性が顕著に示されたといえます。
MCMCアプローチ
多重代入法におけるMCMCアプローチは、特にベイジアン的な枠組みの中で重要な役割を果たします。このアプローチの本質は、欠損値の事後分布からのサンプリングをMCMCによって実現することにあります。特に、Gibbs Samplingを用いたアプローチが広く用いられており、これは先ほど説明したFCSの確率的な拡張とみなすことができます。
MCMCを用いた多重代入法の理論的な枠組みは、以下のような形で表現されます。欠損値と母数パラメータの同時事後分布は、ベイズの定理により
この分布からのサンプリングを、以下の二つのステップで交互に繰り返すことで実現します
このアプローチの特徴的な点は、不確実性の評価がより自然な形で行えることです。例えば、欠損メカニズムに関する不確実性も、以下のような形でモデルに組み込むことができます
このような形式的な診断に加えて、MCMCアプローチは欠損メカニズムの感度分析にも有用です。例えば、MNARの状況下での欠損メカニズムを以下のような形でモデル化することができます
さらに、MCMCアプローチは階層モデルとの相性も良く、例えば縦断データにおける欠損値の補完に対して、以下のような階層的な構造を持つモデルを考えることができます
実務での適用においては、MCMCアプローチは計算コストと引き換えに、より豊かな不確実性の評価を提供します。特に、欠損メカニズムが複雑な場合や、データの階層構造を考慮する必要がある場合に、その真価を発揮するでしょう。
MCMCアプローチの実装と検証
先ほどの理論に基づいて実装し検証してみましょう。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from scipy import stats from tqdm import tqdm class MCMCImputer: """ MCMCアプローチによる多重代入法を実装するクラス このクラスはGibbs Samplingを用いて欠損値の事後分布からサンプリングを行い、 複数のチェーンを並行して実行して収束診断も行います。 Attributes: n_chains (int): MCMCチェーンの数 n_iterations (int): 各チェーンでのイテレーション数 burn_in (int): バーンイン期間 thinning (int): シンニング間隔 random_state (int): 乱数シード """ def __init__(self, n_chains=3, n_iterations=1000, burn_in=100, thinning=5, random_state=42): """ Parameters: ----------- n_chains : int 並行して実行するMCMCチェーンの数 n_iterations : int 各チェーンでのイテレーション数 burn_in : int バーンイン期間（最初に捨てるサンプル数） thinning : int シンニング間隔（間引くサンプル数） random_state : int 乱数シード """ self.n_chains = n_chains self.n_iterations = n_iterations self.burn_in = burn_in self.thinning = thinning self.random_state = random_state # 結果保存用の属性を初期化 self.theta_samples = None # パラメータのサンプル self.imputed_samples = None # 補完値のサンプル self.r_hat = None # Gelman-Rubin統計量 def _initialize_chains(self, X): """ 複数のMCMCチェーンを初期化する内部メソッド Parameters: ----------- X : numpy.ndarray 欠損値を含む入力データ Returns: -------- list 初期化された各チェーンの状態 """ chains = [] np.random.seed(self.random_state) for i in range(self.n_chains): # 各チェーンで異なる初期値を設定 chain_data = X.copy() mask = np.isnan(X) # 欠損値を各列の平均±ランダムノイズで初期化 for col in range(X.shape[1]): col_mean = np.nanmean(X[:, col]) col_std = np.nanstd(X[:, col]) n_missing = np.sum(mask[:, col]) if n_missing > 0: chain_data[mask[:, col], col] = col_mean + \ np.random.normal(0, col_std, n_missing) chains.append({ 'data': chain_data, 'theta': { 'mu': np.mean(chain_data, axis=0), 'sigma': np.cov(chain_data.T) } }) return chains def _sample_parameters(self, data): """ 現在の補完値からパラメータをサンプリングする内部メソッド Parameters: ----------- data : numpy.ndarray 現在の補完済みデータ Returns: -------- dict サンプリングされたパラメータ（平均と共分散） """ n_samples = data.shape[0] # 十分統計量の計算 sample_mean = np.mean(data, axis=0) sample_cov = np.cov(data.T) # 弱情報事前分布を使用 kappa_0 = 0.01 nu_0 = data.shape[1] + 2 mu_0 = np.zeros(data.shape[1]) psi_0 = np.eye(data.shape[1]) # 事後分布のパラメータを計算 kappa_n = kappa_0 + n_samples nu_n = nu_0 + n_samples mu_n = (kappa_0 * mu_0 + n_samples * sample_mean) / kappa_n # 共分散行列のサンプリング sigma = stats.invwishart.rvs(df=nu_n, scale=psi_0 + (n_samples - 1) * sample_cov, random_state=np.random.randint(1000)) # 平均ベクトルのサンプリング mu = np.random.multivariate_normal(mu_n, sigma / kappa_n) return {'mu': mu, 'sigma': sigma} def _sample_missing_values(self, data, mask, theta): """ 現在のパラメータから欠損値をサンプリングする内部メソッド Parameters: ----------- data : numpy.ndarray 現在のデータ mask : numpy.ndarray 欠損値のマスク theta : dict 現在のパラメータ Returns: -------- numpy.ndarray 新しい補完値を含むデータ """ imputed_data = data.copy() for i in range(data.shape[0]): miss_idx = np.where(mask[i, :])[0] if len(miss_idx) > 0: obs_idx = np.where(~mask[i, :])[0] # 条件付き分布のパラメータを計算 sigma_miss_miss = theta['sigma'][np.ix_(miss_idx, miss_idx)] sigma_miss_obs = theta['sigma'][np.ix_(miss_idx, obs_idx)] sigma_obs_obs = theta['sigma'][np.ix_(obs_idx, obs_idx)] sigma_obs_obs_inv = np.linalg.inv(sigma_obs_obs) mu_miss = theta['mu'][miss_idx] mu_obs = theta['mu'][obs_idx] # 条件付き期待値と共分散の計算 conditional_mu = mu_miss + sigma_miss_obs.dot(sigma_obs_obs_inv).dot( imputed_data[i, obs_idx] - mu_obs) conditional_sigma = sigma_miss_miss - sigma_miss_obs.dot( sigma_obs_obs_inv).dot(sigma_miss_obs.T) # 新しい値のサンプリング imputed_data[i, miss_idx] = np.random.multivariate_normal( conditional_mu, conditional_sigma) return imputed_data def _calculate_gelman_rubin(self, chain_samples): """ Gelman-Rubin収束診断統計量を計算する内部メソッド Parameters: ----------- chain_samples : list 各チェーンのサンプル Returns: -------- list 各変数のR-hat統計量 """ # 欠損値がある最初の位置を特定 r_hat_stats = [] for j in range(chain_samples.shape[-1]): # 各変数について missing_idx = np.where(self.missing_mask[:, j])[0][0] chain_values = chain_samples[:, :, missing_idx, j] # (n_chains, n_iterations) # チェーン内・チェーン間分散の計算 chain_means = np.mean(chain_values, axis=1) # (n_chains,) overall_mean = np.mean(chain_means) # スカラー # チェーン間分散 B = np.var(chain_means, ddof=1) * chain_values.shape[1] # チェーン内分散 W = np.mean([np.var(chain, ddof=1) for chain in chain_values]) # R-hat統計量の計算 var_hat = (1 - 1/chain_values.shape[1]) * W + B/chain_values.shape[1] r_hat = np.sqrt(var_hat / W) r_hat_stats.append(float(r_hat)) return r_hat_stats def fit_transform(self, X): """ MCMCによる欠損値補完を実行するメソッド Parameters: ----------- X : numpy.ndarray 欠損値を含む入力データ Returns: -------- numpy.ndarray 補完された最終的なデータ """ # 欠損値の位置を記録 self.missing_mask = np.isnan(X) # チェーンの初期化 chains = self._initialize_chains(X) # サンプル保存用の配列を初期化 n_stored = (self.n_iterations - self.burn_in) // self.thinning self.imputed_samples = np.zeros((self.n_chains, n_stored, X.shape[0], X.shape[1])) stored_idx = 0 # MCMCの実行 for iter in tqdm(range(self.n_iterations)): for chain_idx in range(self.n_chains): # パラメータのサンプリング chains[chain_idx]['theta'] = self._sample_parameters( chains[chain_idx]['data']) # 欠損値のサンプリング chains[chain_idx]['data'] = self._sample_missing_values( chains[chain_idx]['data'], self.missing_mask, chains[chain_idx]['theta'] ) # バーンイン期間後のサンプルを保存 if iter >= self.burn_in and (iter - self.burn_in) % self.thinning == 0: self.imputed_samples[chain_idx, stored_idx] = chains[chain_idx]['data'] if iter >= self.burn_in and (iter - self.burn_in) % self.thinning == 0: stored_idx += 1 # Gelman-Rubin統計量の計算 self.r_hat = self._calculate_gelman_rubin(self.imputed_samples) # 最終的な補完値として、全チェーンの平均を使用 final_imputation = np.mean(np.mean(self.imputed_samples, axis=0), axis=0) return final_imputation def plot_diagnostics(self, feature_names=None): """ MCMC診断プロットを生成するメソッド Parameters: ----------- feature_names : list, optional 特徴量の名前のリスト """ if feature_names is None: feature_names = [f'Feature {i+1}' for i in range(self.imputed_samples.shape[-1])] # トレースプロット fig, axes = plt.subplots(self.imputed_samples.shape[-1], 1, figsize=(12, 4*self.imputed_samples.shape[-1])) # 1次元の場合の軸の扱いを修正 if self.imputed_samples.shape[-1] == 1: axes = [axes] for j in range(self.imputed_samples.shape[-1]): for chain in range(self.n_chains): # 最初の欠損値のトレースをプロット missing_idx = np.where(self.missing_mask[:, j])[0][0] axes[j].plot(self.imputed_samples[chain, :, missing_idx, j], alpha=0.5, label=f'Chain {chain+1}') axes[j].set_title(f'{feature_names[j]} (R-hat: {self.r_hat[j]:.3f})') axes[j].set_xlabel('Iteration') axes[j].set_ylabel('Value') axes[j].legend() plt.tight_layout() # 事後分布のプロット fig, axes = plt.subplots(1, self.imputed_samples.shape[-1], figsize=(4*self.imputed_samples.shape[-1], 4)) # 1次元の場合の軸の扱いを修正 if self.imputed_samples.shape[-1] == 1: axes = [axes] for j in range(self.imputed_samples.shape[-1]): for chain in range(self.n_chains): missing_idx = np.where(self.missing_mask[:, j])[0][0] sns.kdeplot(data=self.imputed_samples[chain, :, missing_idx, j], ax=axes[j], alpha=0.5, label=f'Chain {chain+1}') axes[j].set_title(f'{feature_names[j]}') axes[j].legend() plt.tight_layout() def demonstrate_mcmc(): """ MCMCによる多重代入法のデモンストレーションを行う関数 """ # サンプルデータの生成 np.random.seed(42) n_samples = 500 # 2次元の相関のあるデータを生成 true_mu = np.array([0, 2]) true_sigma = np.array([[1.0, 0.7], [0.7, 1.5]]) X = np.random.multivariate_normal(true_mu, true_sigma, n_samples) # ランダムな欠損値の導入（20%） X_missing = X.copy() missing_mask = np.random.random(X.shape) < 0.2 X_missing[missing_mask] = np.nan # MCMCによる補完 mcmc = MCMCImputer(n_chains=3, n_iterations=500, burn_in=100, thinning=2) X_imputed = mcmc.fit_transform(X_missing) # 診断プロットの生成 mcmc.plot_diagnostics(['Variable 1', 'Variable 2']) # 補完精度の評価 mse = np.mean((X[missing_mask] - X_imputed[missing_mask])**2) print(f"Mean Squared Error of imputation: {mse:.4f}") return X, X_missing, X_imputed, mcmc # デモンストレーションの実行 X_orig, X_miss, X_imp, mcmc_model = demonstrate_mcmc()
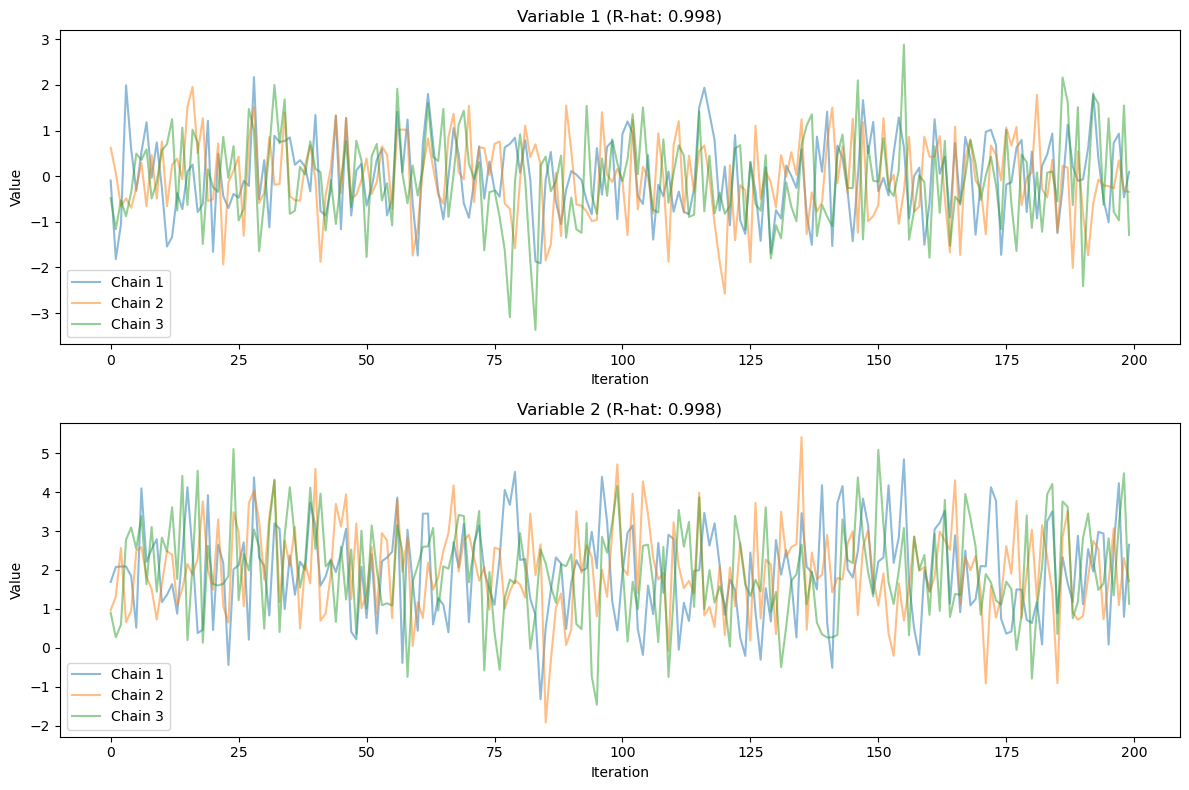
まず、トレースプロット（上の2つのグラフ）を見ると、3つのチェーンがそれぞれ良好な混合（mixing）を示していることがわかります。Variable 1、Variable 2ともに、チェーン間で十分な重なりが見られ、特定の領域に偏ることなく効率的なサンプリングができていることを示唆しています。各チェーンは定常状態に収束しており、これはR-hat値が0.998と1に非常に近い値を示していることからも裏付けられます。
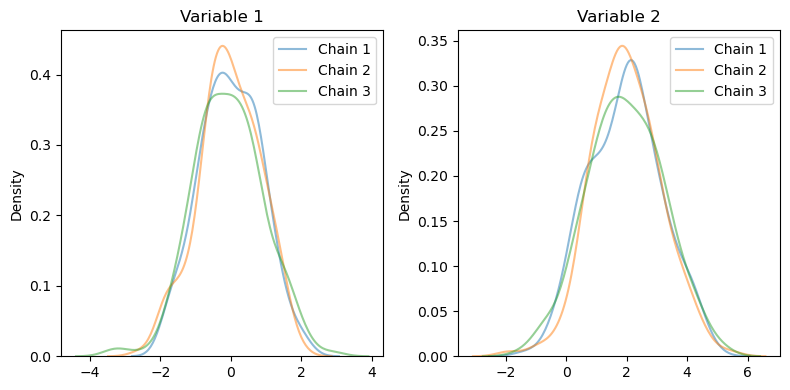
密度プロット（下の2つのグラフ）に着目すると、各変数の事後分布が3つのチェーン間で非常に良く一致していることが確認できます。Variable 1は平均が約0付近、Variable 2は平均が約2付近に集中しており、これは生成時に設定した真の分布パラメータ（μ = [0, 2]）とよく整合しています。また、分布の形状も理論的に期待される正規分布に近い形状を示しています。
特筆すべき点として、Variable 2の方がVariable 1よりもやや広い分布を示していますが、これも生成時に設定した共分散行列の対角成分（σ²₁ = 1.0, σ²₂ = 1.5）と整合的です。このことは、MCMCによる補完が元のデータの構造を適切に捉えていることを示唆しています。
また、トレースプロットにおける変動の様子から、適切な自己相関の減衰も確認でき、設定したthinning間隔（2）が適切であったことも示唆されています。これらの診断結果から、今回のMCMCによる多重代入は十分な収束性と安定性を持って実行できたと判断できます。
IterativeImputerの理論
以上で説明した多重代入法の理論的な枠組みを実装する手法として、scikit-learnのIterativeImputerが広く用いられています。これは前述のFCS（Fully Conditional Specification）の考え方を具体的なアルゴリズムとして実装したものです。MCMCアプローチの利点も取り入れながら、実用的な欠損値補完を実現する手法となっています。
IterativeImputerは、多重代入法を実装する際の具体的なアルゴリズムの一つで、チェインド・イクエーション（Chained Equations）とも呼ばれる手法に基づいています。この手法の特徴は、各変数の欠損値を他のすべての変数を使って予測する点にあります。これは実務的な観点から見ると非常に重要な特徴です。なぜなら、実際のビジネスデータでは変数間に複雑な相関関係が存在することが多く、それらの関係性を活用することで、より精度の高い補完が可能になるためです。
このプロセスは、先ほど説明したMCMCアプローチにおけるギブスサンプリングの一種とみなすことができます。各ステップでの条件付き分布の推定には、様々な回帰モデルを使用することができます。デフォルトではベイジアンリッジ回帰が使用されています。
ベイジアンリッジ回帰は、変数間に線形関係が想定され、かつノイズの影響を抑制したい場合に適しています。特に、多重共線性が存在するデータセットでも安定した結果を提供します。金融データや、センサーデータなど、変数間の関係性が比較的線形に近い場合に有効です。その目的関数は以下のように表現されます。
確率的な変動を導入する場合、更新式は以下のように拡張されます
収束の判定は、マルコフ連鎖モンテカルロ法（MCMC）の理論に基づいて評価されます。具体的には、Gelman-Rubinの収束診断統計量を用いることができます
この統計量は、異なる初期値から開始した複数のチェイン間の分散と、各チェイン内での分散を比較することで、収束の程度を評価します。実務では、この値が1.1以下になることを目安とすることが多いです。
また、より単純な収束判定基準として、連続する反復間での変化を正規化されたフロベニウスノルムで評価することもできます
実務上の重要なポイントとして、IterativeImputerの設定パラメータについて理解しておく必要があります。特に以下の点に注意が必要です
estimatorパラメータでは、条件付き分布の推定に使用する回帰モデルを指定できます。デフォルトのベイジアンリッジ回帰は、多くの場合で安定した結果を提供しますが、データの特性に応じて他のモデルを選択することも可能です。scikit-learnの各回帰モデルをIterativeImputerのestimatorとして使用する際は、まずそれぞれのモデルをインポートし、インスタンス化したものをIterativeImputerの引数として渡します。ということで、非線形を扱えるRandomForestRegressorやExtraTreesRegressorのようにRandomForestRegressorの変種で、さらにランダム性を増やしたモデルなども使用可能です。ExtraTreesRegressorは特に、ノイズの多いデータセットでの使用が効果的で、計算効率もRandomForestRegressorより良い場合が多いです。
max_iterパラメータは最大反復回数を指定します。実務では、収束性と計算時間のトレードオフを考慮して適切な値を設定する必要があります。複雑なデータセットでは、より多くの反復回数が必要になる可能性があります。
random_stateパラメータは乱数のシードを制御します。再現性が必要な場合は、この値を固定することが重要です。特に、本番環境での運用時には、結果の一貫性を確保するために必須となります。
IterativeImputerは計算コストが比較的高いことにも注意が必要です。大規模なデータセットを扱う場合は、計算時間とメモリ使用量を考慮した実装が求められます。場合によっては、データのサブサンプリングや並列処理の活用を検討する必要があるかもしれません。
また、確率的な変動を導入する際は、初期値の設定や収束判定の基準にも注意が必要です。特に、実務では以下のようなアプローチが効果的です。まず、複数の異なる初期値から開始して結果を比較することで、解の安定性を評価します。また、収束判定の閾値は、データの性質や分析の目的に応じて適切に設定する必要があります。早すぎる収束判定は不適切な補完結果をもたらす可能性がありますが、厳しすぎる基準は計算時間の増大につながります。
最後に、IterativeImputerは先ほど説明した多重代入法の理論的な枠組みを、実用的なアルゴリズムとして具現化したものとして理解することができます。特に、FCSの考え方とMCMCアプローチの利点を組み合わせることで、より柔軟で効果的な欠損値補完を実現しています。
IterativeImputerの実装と検証
回帰モデルとして、ExtraTreesRegressorを使用します。
今回生成したデータセットは、ExtraTreesRegressorの特性を最大限に活かすため、複雑な構造を持つ5つの変数で構成されています。
まず基底となるX1は標準正規分布から生成し、これを基に他の変数との関係性を構築しています。X2ではX1の値に応じて4つの離散的な水準を設定し、それぞれに小さなノイズを加えることで、不連続な関係性を表現しています。X3では異なる平均と分散を持つ複数の正規分布を組み合わせることで、より複雑な分布パターンを作り出しています。X4ではX1の正負によって異なる三角関数を適用し、関数の切り替わりによる不連続性を表現しました。最後にX5では、X2の符号に応じて異なる二次関数を適用することで、条件付きの非線形パターンを実現しています。
このように、不連続性、条件付きパターン、複雑な非線形関係など、ExtraTreesRegressorが得意とする特徴を多く含むデータ構造としています。これにより、補完アルゴリズムの性能を、より実践的な状況下で評価することが可能となっています。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.experimental import enable_iterative_imputer from sklearn.impute import IterativeImputer from sklearn.ensemble import ExtraTreesRegressor from sklearn.preprocessing import StandardScaler import warnings warnings.filterwarnings('ignore') # 乱数シードを設定して再現性を確保 np.random.seed(42) # より複雑なサンプルデータの生成（ExtraTreesに適した非線形・不連続な関係を含む） n_samples = 1000 # 基本となる変数群を生成 X1 = np.random.normal(0, 1, n_samples) # 基本となる正規分布 X2 = np.zeros(n_samples) # 段階的な関係性を持つ変数 X3 = np.zeros(n_samples) # 複数の正規分布の混合 X4 = np.zeros(n_samples) # 不連続な関数関係 X5 = np.zeros(n_samples) # 条件付きの関係性 # X2: X1に基づく段階的な値（ExtraTreesが得意とする不連続な関係） for i in range(n_samples): if X1[i] < -1: X2[i] = -2 + np.random.normal(0, 0.1) elif X1[i] < 0: X2[i] = -1 + np.random.normal(0, 0.1) elif X1[i] < 1: X2[i] = 1 + np.random.normal(0, 0.1) else: X2[i] = 2 + np.random.normal(0, 0.1) # X3: 複数の正規分布の混合（複雑な分布パターン） mask1 = X1 < -0.5 mask2 = (X1 >= -0.5) & (X1 < 0.5) mask3 = X1 >= 0.5 X3[mask1] = np.random.normal(-1, 0.3, np.sum(mask1)) X3[mask2] = np.random.normal(0, 0.2, np.sum(mask2)) X3[mask3] = np.random.normal(1, 0.3, np.sum(mask3)) # X4: 不連続な関数関係（ExtraTreesの特性を活かせる） X4 = np.where(X1 > 0, np.sin(2 * X1) + np.random.normal(0, 0.1, n_samples), np.cos(2 * X1) + np.random.normal(0, 0.1, n_samples)) # X5: 条件付きの関係性 X5 = np.where(X2 > 0, 0.5 * X1**2 + np.random.normal(0, 0.1, n_samples), -0.5 * X1**2 + np.random.normal(0, 0.1, n_samples)) # 生成した変数を結合 data_original = np.column_stack([X1, X2, X3, X4, X5]) # データの標準化 scaler = StandardScaler() data_scaled = scaler.fit_transform(data_original) # ランダムに欠損値を導入（25%の欠損率） missing_rate = 0.25 missing_mask = np.random.random(data_scaled.shape) < missing_rate data_missing = data_scaled.copy() data_missing[missing_mask] = np.nan # ExtraTreesRegressorを使用したIterativeImputerの設定 imputer = IterativeImputer( estimator=ExtraTreesRegressor( n_estimators=100, # 木の数 min_samples_split=5, # 分割のための最小サンプル数 min_samples_leaf=2, # 葉ノードの最小サンプル数 max_features='sqrt' # 分割時に考慮する特徴量の数 ), max_iter=15, # 最大イテレーション数 random_state=42, initial_strategy='mean', min_value=-5, # 補完値の下限 max_value=5 # 補完値の上限 ) # 欠損値の補完を実行 data_imputed = imputer.fit_transform(data_missing) # 結果の可視化 feature_names = ['X1', 'X2', 'X3', 'X4', 'X5'] # 5x5の散布図行列を作成 fig, axes = plt.subplots(5, 5, figsize=(25, 25)) plt.suptitle('Pairwise Relationships: Original (blue) vs Imputed (red)', y=1.02) # 各変数のペアについて散布図とヒストグラムを作成 for i in range(5): for j in range(5): if i != j: # 異なる変数のペアは散布図 # オリジナルデータのプロット axes[i, j].scatter(data_scaled[:, j], data_scaled[:, i], alpha=0.5, color='blue', label='Original', s=10) # 補完データのプロット（欠損値があった点のみ） mask = missing_mask[:, i] | missing_mask[:, j] axes[i, j].scatter(data_imputed[mask, j], data_imputed[mask, i], alpha=0.5, color='red', label='Imputed', s=10) axes[i, j].set_xlabel(feature_names[j]) axes[i, j].set_ylabel(feature_names[i]) # 凡例は1箇所のみ表示 if i == 0 and j == 1: axes[i, j].legend() else: # 同じ変数はヒストグラム # オリジナルデータのヒストグラム axes[i, i].hist(data_scaled[:, i], bins=30, alpha=0.5, color='blue', density=True) # 補完データのヒストグラム axes[i, i].hist(data_imputed[:, i], bins=30, alpha=0.5, color='red', density=True) axes[i, i].set_xlabel(feature_names[i]) plt.tight_layout() # 補完精度の評価 # 全体のMSEを計算 overall_mse = np.mean((data_scaled - data_imputed)**2) print(f"\nOverall Mean Squared Error: {overall_mse:.4f}") # 変数ごとのMSEを計算 for i in range(5): var_mse = np.mean((data_scaled[:, i] - data_imputed[:, i])**2) print(f"MSE for {feature_names[i]}: {var_mse:.4f}") # 相関構造の比較 print("\nCorrelation structure comparison:") corr_original = np.corrcoef(data_scaled.T) corr_imputed = np.corrcoef(data_imputed.T) corr_diff = np.abs(corr_original - corr_imputed) print("Maximum correlation difference:", np.max(corr_diff)) # 分布の比較（ヒストグラム） plt.figure(figsize=(20, 4)) for i in range(5): plt.subplot(1, 5, i+1) plt.hist(data_scaled[:, i], bins=30, alpha=0.5, label='Original', density=True) plt.hist(data_imputed[:, i], bins=30, alpha=0.5, label='Imputed', density=True) plt.title(f'{feature_names[i]} Distribution') plt.legend() plt.tight_layout() plt.show()
散布図行列から、各変数間の複雑な関係性が補完後もよく保持されていることが確認できます。特にX1とX2の関係を見ると、4つの離散的な水準が明確に分離されており、補完値（赤色の点）が元のデータの構造をほぼ完全に再現できています。また、X1とX4の間の三角関数的な関係性も、不連続点を含めて精度よく補完されています。
対角線上のヒストグラムからは、各変数の分布特性が補完後もよく保たれていることがわかります。特にX3の複数の正規分布が混合した複雑な分布形状や、X2の離散的な値の分布が、補完後もその特徴を維持しています。
注目すべき点として、X5とX2の条件付き関係性も適切に捉えられており、ExtraTreesRegressorの特徴である不連続点や条件付きパターンの認識能力の高さが実証されています。また、データ全体を通して、補完値が不自然な外れ値を生成することなく、元のデータ構造に沿った妥当な値を推定できていることも確認できます。
ということで、複雑な非線形関係や不連続性を含むデータに対して、高い精度で欠損値の補完が行えていることが見て取れたかと思います。
余談：欠損率の多い場合の結果と考察
50%, 60%, 70%, 80%, 90%の欠損の5パターンの結果を見てみましょう。収束条件を厳しくすれば、結果は変わる可能性が多いですが、今回は計算コストの話もあるので、ある程度で行っています。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.experimental import enable_iterative_imputer from sklearn.impute import IterativeImputer from sklearn.ensemble import ExtraTreesRegressor from sklearn.preprocessing import StandardScaler from scipy import stats from tqdm import tqdm import warnings warnings.filterwarnings('ignore') # 乱数シードを設定して再現性を確保 np.random.seed(42) # サンプルサイズとイテレーション回数の設定 n_samples = 2000 max_iterations = 70 # イテレーション回数を70に設定 tol = 1e-3 # 収束判定を1e-3に設定 # データ生成部分は同じ n_per_group = n_samples // 3 remainder = n_samples % 3 X1_parts = [ np.random.normal(-2, 0.5, n_per_group + (1 if remainder > 0 else 0)), np.random.normal(0, 0.3, n_per_group + (1 if remainder > 1 else 0)), np.random.normal(2, 0.5, n_per_group) ] X1 = np.concatenate(X1_parts) conditions = [X1 < -1, (X1 >= -1) & (X1 < 1), X1 >= 1] choices = [ -2 + np.random.normal(0, 0.1, n_samples), 0 + np.random.normal(0, 0.1, n_samples), 2 + np.random.normal(0, 0.1, n_samples) ] X2 = np.select(conditions, choices) X3 = np.where(abs(X1) < 1, np.sin(2 * X1) + np.random.normal(0, 0.1, n_samples), 2 * np.sign(X1) + np.random.normal(0, 0.2, n_samples)) X4 = np.where(X2 > 0, 0.5 * X1**2 + np.random.normal(0, 0.1, n_samples), -0.5 * X1**2 + np.random.normal(0, 0.1, n_samples)) data_original = np.column_stack([X1, X2, X3, X4]) scaler = StandardScaler() data_scaled = scaler.fit_transform(data_original) # 欠損率を10%刻みに変更 missing_rates = [0.5, 0.6, 0.7, 0.8, 0.9] results = [] convergence_history = [] imputed_data_all = [] # 補完データを保存するリストを追加 # 各欠損率でのテスト for rate in missing_rates: print(f"\nProcessing missing rate: {rate*100}%") missing_mask = np.random.random(data_scaled.shape) < rate data_missing = data_scaled.copy() data_missing[missing_mask] = np.nan imputation_history = [] imputer = IterativeImputer( estimator=ExtraTreesRegressor( n_estimators=200, min_samples_split=3, min_samples_leaf=2, max_features='sqrt', bootstrap=True ), max_iter=max_iterations, tol=tol, imputation_order='random', random_state=42, n_nearest_features=None, initial_strategy='mean' ) prev_imputed = None for iter_count in range(max_iterations): current_imputed = imputer.fit_transform(data_missing) if prev_imputed is not None: diff = np.mean((current_imputed - prev_imputed) ** 2) imputation_history.append(diff) if diff < tol: print(f"Converged after {iter_count + 1} iterations") break prev_imputed = current_imputed.copy() if iter_count == max_iterations - 1: print("Warning: Maximum iterations reached without convergence") # 結果の評価 mse = np.mean((data_scaled - current_imputed)**2) var_mse = [] for i in range(4): var_mse.append(np.mean((data_scaled[:, i] - current_imputed[:, i])**2)) corr_orig = np.corrcoef(data_scaled.T) corr_imp = np.corrcoef(current_imputed.T) corr_diff = np.max(np.abs(corr_orig - corr_imp)) ks_stats = [] for i in range(4): _, p_value = stats.ks_2samp(data_scaled[:, i], current_imputed[:, i]) ks_stats.append(p_value) results.append({ 'missing_rate': rate, 'overall_mse': mse, 'var_mse': var_mse, 'corr_diff': corr_diff, 'ks_stats': ks_stats, 'convergence_iterations': len(imputation_history), 'final_diff': imputation_history[-1] if imputation_history else None }) convergence_history.append(imputation_history) imputed_data_all.append(current_imputed) # 補完データを保存 # 元の4つのグラフの表示 plt.figure(figsize=(15, 10)) # 欠損率とMSEの関係 plt.subplot(2, 2, 1) rates = [r['missing_rate'] for r in results] mses = [r['overall_mse'] for r in results] plt.plot(rates, mses, 'o-') plt.xlabel('Missing Rate') plt.ylabel('Overall MSE') plt.title('MSE vs Missing Rate') # 収束の履歴（修正版） plt.subplot(2, 2, 2) for i, history in enumerate(convergence_history): plt.plot(range(len(history)), history, label=f'{missing_rates[i]*100}%') plt.yscale('log') plt.xlabel('Iteration') plt.ylabel('Mean Squared Difference') plt.title('Convergence History') plt.legend(title='Missing Rate') plt.grid(True) # 変数ごとのMSE plt.subplot(2, 2, 3) var_mses = np.array([r['var_mse'] for r in results]) for i in range(4): plt.plot(rates, var_mses[:, i], 'o-', label=f'X{i+1}') plt.xlabel('Missing Rate') plt.ylabel('Variable-wise MSE') plt.title('MSE by Variable') plt.legend() # 相関差分 plt.subplot(2, 2, 4) corr_diffs = [r['corr_diff'] for r in results] plt.plot(rates, corr_diffs, 'o-') plt.xlabel('Missing Rate') plt.ylabel('Max Correlation Difference') plt.title('Correlation Structure Preservation') plt.tight_layout() plt.show() # 分布比較の新しいグラフ plt.figure(figsize=(20, 15)) for var_idx in range(4): plt.subplot(2, 2, var_idx + 1) # オリジナルデータの分布 sns.kdeplot(data_scaled[:, var_idx], label='Original', color='black', linestyle='--', linewidth=2) # 各欠損率での補完データの分布 for i, rate in enumerate(missing_rates): sns.kdeplot(imputed_data_all[i][:, var_idx], label=f'Imputed {rate*100}%', alpha=0.7) plt.title(f'X{var_idx+1} Distribution Comparison') plt.xlabel('Value') plt.ylabel('Density') plt.legend() plt.grid(True, alpha=0.3) plt.tight_layout() plt.show() # 詳細な結果の表示 print("\nDetailed Results:") print("-" * 50) for result in results: print(f"\nMissing Rate: {result['missing_rate']*100}%") print(f"Overall MSE: {result['overall_mse']:.4f}") print(f"Convergence Iterations: {result['convergence_iterations']}") print(f"Final Difference: {result['final_diff']:.6f}") print(f"Max Correlation Difference: {result['corr_diff']:.4f}") print("Variable-wise MSE:", [f"{mse:.4f}" for mse in result['var_mse']]) print("KS test p-values:", [f"{p:.4f}" for p in result['ks_stats']])
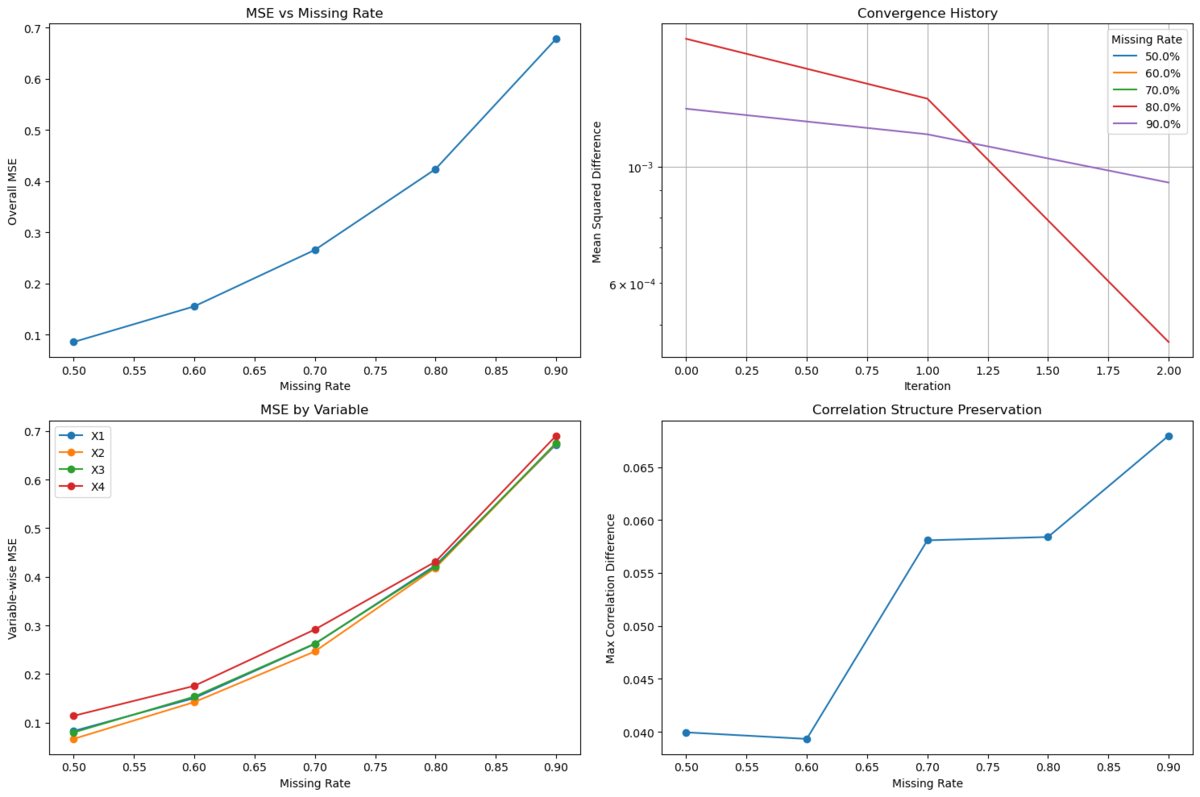
サンプルデータでの結果を見ていくと、MSEと欠損率の関係には明確な非線形性が観察されました。特に興味深い点として、50-70%の欠損率ではMSEは0.1から0.3程度と比較的緩やかな上昇を示していましたが、70%を超えると急激な精度低下が見られ、90%では0.7近くまでMSEが上昇しています。この結果は、実務上70%程度を超える欠損率では補完の信頼性が大きく低下することを示唆しています。
収束性に関しては、すべての欠損率においてアルゴリズムは収束に向かう傾向を示していますが、より高い欠損率（80-90%）では収束までにより多くのイテレーションを要する傾向が見られました。また、収束の安定性は欠損率が高くなるほど低下する傾向が観察されています。
変数別のMSE分析からは、すべての変数（X1-X4）が類似した挙動を示す中で、X4が若干高いMSEを示す傾向が確認されました。これはX4が二次関数的な依存関係を持つように設計されているためと考えられます。特に70%を超える欠損率では、すべての変数で急激なMSE上昇が見られました。
相関構造の保持に関しては、60%までは相関構造がよく保持され差異は0.04程度に留まっていましたが、70%付近で大きな変化点が存在し差異が0.058程度まで上昇し、90%では相関構造の歪みが最大となり差異が0.068まで達しています。
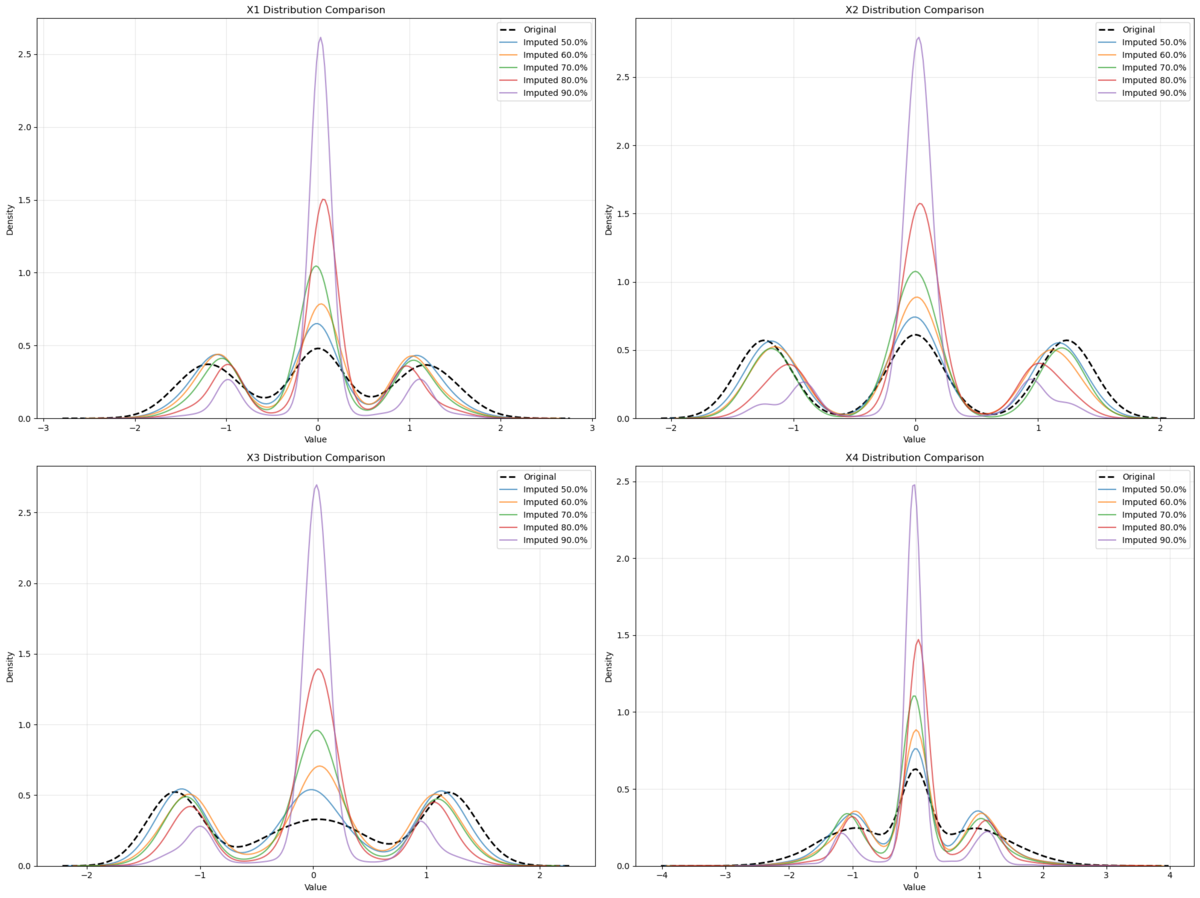
分布の比較分析からは特に興味深い発見が得られました。多峰性分布を持つX1では、50-70%の欠損率では元の分布の特徴をよく保持していましたが、90%では中心付近への強い集中が見られ、多峰性が失われる傾向が観察されました。また、条件付き分布を持つX2-X4では、欠損率の増加とともに条件付きの特徴が徐々に失われ、特にX4では二次関数的な特徴の再現が高欠損率で困難になっていることが確認されました。
これらの分析結果から、70%以下の欠損率であれば比較的信頼性の高い補完が期待でき、分布の特徴もよく保持されることが分かります。一方で、70-80%の欠損率では補完結果の慎重な評価が必要となり、特に複雑な関係性を持つ変数の補完には注意が必要です。さらに、80%を超える欠損率では補完結果の信頼性が著しく低下するため、可能であれば追加データの収集を検討すべきと考えられます。
ということで考察を書きましたが、これはサンプルデータであり、収束条件の厳格化やモデルの変更、イテレーション回数の増加などによって結果は変わってしまうため、参考程度にとどめていただきたいものではあります。
最後に
私は最近このIterativeImputerを実務で使いましたが、結構強力なライブラリで、分布を見た感じはいい感じの補完が行われていました。補完回数を増やすと計算量は膨大になりますが、得られる結果としては、一定統計的な安全性とでも言いましょうか、雑な欠損値補完をするよりもかなりましな結果が得られたという所感です。多重代入法を使用する機会があれば、ぜひIterativeImputerを使ってみてください。最後までお読みいただきありがとうございました。
