はじめに

前回混合ガウスモデル（GMM）に関する記事を書かさせていただきました。今回は、混合ガウスモデルから考え方を派生させて、クラスタリングに使用する各変数によって、仮定する確率分布を柔軟に変化させ、柔軟な確率的アプローチなクラスタリングを実装できないかというのが今回の、記事の趣旨になってきます。この発想自体は、私の発想ではなく、仕事の中で同僚が考えた方法であり、私はそれを少し聞きかじった程度の状態で、自分の中で想像を膨らませ、今回考えた手法（仮に混合確率分布モデルとする）を理論と実装にわたり軽く記事にしてみようというのが今回の趣旨になってきます。
そもそも、GMM自体が近年流行してきている、ベイズ統計学的な考え方に基づいて、理論が成り立っていたわけですが、今回はさらにベイズ統計学的な発想にのっとた手法となるわけです。個人的には、とても魅力的な理論であり、実用できるのであれば、大変有用な手法であるなと感じているのですが、実際のところどの程度使用できるのかは、未知数というところで、結果がどのようになるのかは、記事を書き始めている現在はまだわかりません。
ただ、今回の混合確率分布モデルによるクラスタリングのような話は、別の場所で聞いたことがないため、今回記事としてまとめることができれば、データサイエンス界隈の人々が、少しは興味を持ってくれる内容なのかな？とは感じています。
とはいえ、この記事を執筆しているのは、データサイエンティストになって間もない若造であり、数学がとても苦手な人物なので、私の頭の中で思い描いた理論と実装というものが、そもそも間違っている可能性というのは、皆様に事前に理解していただいたうえで読んでいただけると幸いです。というより、私よりも超絶優秀な人々が、記事を読みに来る気がするので、こうしたほうがもっといいんじゃないか？みたいな話があればどんどん突っ込んで来てほしいです。正直いつもの記事は、論文などを参照しながら書いているので、気楽に書いているのですが、今回は、混合ガウスモデルという大元となる手法からの派生とはいえ、理論部分も含めて自分一人で空想していくわけなので、どの辺まで確からしいものに仕上がるかは本当に未知数です。
では本題へと入っていきましょう。混合ガウスモデル（GMM）に関する記事は以下に貼っておきます。

tomtom58.hatenablog.com

混合確率分布モデルの理論

モデルの概要

はじめにの部分であらかた書きましたが、今回は混合ガウスモデル（GMM）の考え方を拡張し、異なるタイプの変数に対して適切な確率分布を仮定します。各クラスタは、これらの確率分布の組み合わせとして表現されることとなります。
前提として、概念的なこのモデルに関する説明をするとするならば、各クラスタが様々な確率分布の組み合わせによって表現されるということは、非常に柔軟であり、確率分布の選定が正しく行われたという前提に立つのであれば、情報を正しく反映された確率的なクラスターが形成されることになるという風に解釈できます。
例えば、顧客セグメンテーションの文脈では、あるクラスタが「年齢は正規分布に従い平均が35歳、収入はガンマ分布に従い平均が5万ドル、製品購入頻度はポアソン分布に従い平均が月2回」というように特徴づけられるかもしれません。このような表現により、各クラスタは単純な中心点や代表値だけでなく、変数間の関係性や分布の形状も含めた豊かな情報を提供します。

メリット・デメリット

次に、この手法の利点と欠点に関して考えてみましょう。この手法の最も大きな利点は、その柔軟性とデータの複雑性に対する高い適応力だという風に考えられます。混合ガウスモデル（GMM）では基本的に連続値のみしか扱えませんでした。これは名称からもわかる通り、すべての変数にガウス分布を規定していたことによって、基本的に連続値しか扱えなかったわけです。ですが、今回の手法では、各変数に最適な確率分布を規定するというアプローチのため、カテゴリカルな変数や、二値変数、連続値まで幅広い情報のデータを活用できるということになります。また、連続値に関しても、ガウス分布のみならず、適切な確率分布を規定することができるという部分が、柔軟性と複雑性への対処ができるという部分になってくると考えられます。
さらに、特にベイズアプローチを用いる場合、パラメータの不確実性を直接モデル化し、推論に組み込むことが可能となってきます。というよりそもそも、不確実性の部分は、混合ガウスモデルの拡張として、確率的なアプローチをとっているため、各クラスターに属する確率という形で、ソフトクラスタリングを実施でき、不確実性を表現することは可能になっています。また、適切な確率分布（例えば重裾分布）を選択することによって、GMMで問題となっていた外れ値の影響を軽減できるという利点も考えられます。
次に、デメリットに関して考えてみましょう。まず、大前提として、複数の確率分布を組み合わせることによって、計算の複雑性が増大し、特に大規模データセットや高次元データの場合に計算量が大きくなることが考えられます。また、混合ガウスモデルの場合は、正規分布を規定する上での制約に関してのみ気を付けていればよかったのに対して、各変数にに対して適切な確率分布を選択する必要があるという部分があります。この部分が一番ネックになってくる気もしますね...適切な確率分布を規定できるかは正直なところ、分析者の腕にだいぶ依ってくるためです。このようにパラメトリックに確率分布を規定しない、カーネル法を使用したGMMの拡張があることも知っていますが、そちらはそちらで、こちらの方法よりも、高次元のデータに対して弱いなど問題を抱えており、実務的には問題をはらんでいるので、適切な確率分布の規定さえできれば、とても良いクラスタリングが行える可能性が非常に高いこの手法に個人的にはとても期待しているという部分もあります。
また、多数の異なる確率分布を組み合わせると、結果の解釈が非常に複雑になってしまうという可能性ははらんでいるのかなと感じます。モデルの柔軟性が高いというのは、表裏一体であり、適切な正則化や評価手法を用いないと、ノイズにも適合してしまう過剰適合のリスクも存在すると考えられます。特にEMアルゴリズムを用いる場合は、局所最適解に陥る可能性があり、初期値の選択が重要になるという課題があります。

前提と仮定

混合確率分布モデル（MPDMとする）はまず、データ生成プロセスに関する仮定があります。このモデルでは、各データポイントが潜在的なクラスタ（または成分）のいずれから生成されると仮定します。具体的には、まずクラスタが確率的に選択され、次にそのクラスタに対応する確率分布からデータ点が生成されるというプロセスを想定しています。
重要な前提の一つに条件付き独立性の仮定があります。これは、与えられたクラスタ内では、各変数が互いに独立であるという仮定です。この仮定により、クラスタ内での各変数の確率分布を個別にモデル化し、それらの積をとることでデータ点の尤度を計算することができます。しかし、この仮定は現実のデータでは完全に成り立つことはほぼ不可能といってもいいでしょう。そのため、変数間の相関を無視してしまう可能性があるということに注意が必要です。
また、混合モデルの識別可能性も重要な前提です。これは、異なるパラメータの組み合わせが同じ確率分布を生成しないという条件です。識別可能性が満たされない場合、モデルのパラメータを一意に推定することが困難になります。
最後は、選択された確率分布が、実際おデータ生成プロセスを適切に表現できるという仮定も重要です。これに関しては、先ほど述べたので割愛します。

どんな変数にはどの確率分布を？

カテゴリカル変数用の分布

多項分布

多項分布は、複数の排他的な事象の出現確率を表す離散的確率分布です。カテゴリカル分布は多項分布の特殊ケースで、1回の試行結果を表します。
数式表現

$P(X = x) = \frac{n!}{x_1! \cdots x_k!} p_1^{x_1} \cdots p_k^{x_k}$

ここで

・ $n$ は試行回数

・ $k$ はカテゴリの数

・ $x_i$ は $i$ 番目のカテゴリが選ばれる回数

・ $p_i$ は $i$ 番目のカテゴリが選ばれる確率

カテゴリカル分布の場合、 $n=1$ となり、一つのカテゴリのみが1他は0となります。

ベルヌーイ分布

ベルヌーイ分布は、二値変数（0か1の値をとる変数）のモデル化に使用される離散確率分布です。これは多項分布の特殊ケース（ $k=2$ ）とも考えられます。

確率質量関数

$P(X = x) = p^x (1-p)^{1-x}$

ここで

・ $x$ は0または1の値

・ $p$ は成功確率（ $x=1$ となる確率）

ベルヌーイ分布は、Yes/No型の質問や成功/失敗のような二値の結果をモデル化するのに適しています。

連続値変数用の分布

正規分布

正規分布に関して説明する必要があるのかは微妙（というか各分布の説明なんてこの記事を読む人には必要ないんじゃ...とはいいつつも初学者向けの記事というのがテーマなので書きます！）
正規分布は、連続値データに広く使用される対称な釣鐘型の分布です。t分布のnが大きい時の分布とも言えますね。
確率密度関数

$f(x|\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

ここで、

・ $\mu$ は平均

・ $\sigma$ は標準偏差

・ $x$ は変数値

正規分布は、中心極限定理により多くの自然現象や測定誤差を表現するのに適しています。

ガンマ分布

ガンマ分布は、正の実数値をとる連続確率分布で、待ち時間や寿命などの減少のモデル化に使用されます。
確率密度関数

$f(x|k,\theta) = \frac{x^{k-1}e^{-\frac{x}{\theta}}}{\theta^k\Gamma(k)}$

ここで

・ $k$ は形状パラメータ

・ $\theta$ は尺度パラメータ

・ $\Gamma(k)$ はガンマ関数

・ $x$ は変数値（ $x>0$ ）

ガンマ分布は、指数分布やカイ二乗分布の一般化として捉えることができます。
他にも色々確率分布はありますが、この辺でやめておこうと思います。

混合モデルの理論

混合確率分布モデルでは、データ点 $x_i$ が $K$ 個のクラスタのいずれかから生成されると仮定します。各クラスタは、異なる確率分布の組み合わせで表現されます。

全体の尤度関数

$f(x|k,\theta) = \frac{x^{k-1}e^{-\frac{x}{\theta}}}{\theta^k\Gamma(k)}$

ここで

・ $N$ はデータ点の総数

・ $K$ はクラスタ数

・ $pi_k$ は $k$ 番目クラスタの混合比率

・ $\theta_k$ は $k$ 番目のクラスターのパラメータセット

・ $P(x_i|\theta_k)$ は $k$ 番目クラスターにおける $x_i$ の確率（または確率密度）

$P(x_i|\theta_k)$ は、各変数の確率分布の積として表現される

$P(x_i | \theta_k) = \prod_{j=1}^M P(x_{ij} | \theta_{kj})$

ここで、 $M$ は変数の数、 $x_{ij}$ は $i$ 番目の変数、 $\theta$ は対応するパラメータです。

この尤度関数は、データが生成されるプロセスを数学的に表現しており、モデルは、この尤度関数を最大化するパラメータを探索することで、データ構造を学習します。

パラメータの推定アプローチ

EMアルゴリズム

EMアルゴリズム（Expectation-Maximization Algorithm）は、潜在変数を含む確率モデルのパラメータを最尤推定する反復アルゴリズムです。混合確率分布モデルの場合、各データ点のクラスタ所属が潜在変数となります。EMアルゴリズムに関しては、混合ガウスモデルの記事にて、もう少し柔らかく詳しく解説したと思うので、GMMの記事を参照していただけるといいと思います。

tomtom58.hatenablog.com

EMアルゴリズムは、E-stepとM-stepを交互に繰り返すことで、パラメータの推定を行います。収束条件などはGMMの記事で解説しているため、今回はE-stepと、M-stepに関して軽く説明するのみとしたいと思います。
　　
Expectation step (E-step):
現在のパラメータ推定値を使用して、各データ点のクラスタ所属確率を計算します。

$\gamma_{ik} = P(z_i = k | x_i, \theta, \pi) = \frac{\pi_k P(x_i | \theta_k)}{\sum_{j=1}^K \pi_j P(x_i | \theta_j)}$

ここで、 $z_i$ は $i$ 番目のデータ点のクラスタ割り当てを表す潜在変数です。

　　
Maximization step (M-step): E-stepで計算した所属確率を使用して、モデルパラメータを更新します。

$\pi_k^{new} = \frac{1}{N} \sum_{i=1}^N \gamma_{ik}$

各確率分布のパラメータ更新は、分布の種類によって異なりますが、一般的に以下の形式になります。

$\theta_k^{new} = \arg\max_{\theta_k} \sum_{i=1}^N \gamma_{ik} \log P(x_i | \theta_k)$

EMアルゴリズムは、対数尤度が収束するまで、または指定した回数まで繰り返されます。　　
例：顧客セグメンテーションモデル
このモデルでは、以下の4つの変数を考慮します
1. 年齢（正規分布）
2. 年間支出額（ガンマ分布）
3. 好みの商品カテゴリ（多項分布）
4. ロイヤリティプログラム加入状況（ベルヌーイ分布）

各クラスター $k$ に対して、尤度関数は以下のように表されます

$P(x_i | \theta_k) = P(x_{i1} | \mu_k, \sigma_k) \cdot P(x_{i2} | \alpha_k, \beta_k) \cdot P(x_{i3} | p_k) \cdot P(x_{i4} | q_k)$

ここで　　
正規分布（年齢）

$P(x_{i1} | \mu_k, \sigma_k) = \frac{1}{\sigma_k\sqrt{2\pi}} \exp\left(-\frac{(x_{i1}-\mu_k)^2}{2\sigma_k^2}\right)$

　　
ガンマ分布（年間支出額）

$P(x_{i2} | \alpha_k, \beta_k) = \frac{\beta_k^{\alpha_k}}{\Gamma(\alpha_k)} x_{i2}^{\alpha_k-1} e^{-\beta_k x_{i2}}$

　　
多項分布（好みの商品カテゴリ）

$P(x_{i3} | p_k) = \frac{n_i!}{x_{i31}!x_{i32}!\cdots x_{i3L}!} p_{k1}^{x_{i31}} p_{k2}^{x_{i32}} \cdots p_{kL}^{x_{i3L}}$

　　
ベルヌーイ分布（ロイヤルティプログラム加入状況）

$P(x_{i4} | q_k) = q_k^{x_{i4}} (1-q_k)^{1-x_{i4}}$

　　
EMアルゴリズムの各ステップは以下のようになります。
E-step

各データ点 $i$ に対して、各クラスタ $k$ への所属確率を計算します

$\gamma_{ik} = \frac{\pi_k P(x_{i1} | \mu_k, \sigma_k) P(x_{i2} | \alpha_k, \beta_k) P(x_{i3} | p_k) P(x_{i4} | q_k)}{\sum_{j=1}^K \pi_j P(x_{i1} | \mu_j, \sigma_j) P(x_{i2} | \alpha_j, \beta_j) P(x_{i3} | p_j) P(x_{i4} | q_j)}$

　　
M-step

各クラスタ $k$ に対して、パラメータを更新します

1. 混合比率： $\pi_k^{new} = \frac{1}{N} \sum_{i=1}^N \gamma_{ik}$

2. 正規分布パラメータ：

$\mu_k^{new} = \frac{\sum_{i=1}^N \gamma_{ik} x_{i1}}{\sum_{i=1}^N \gamma_{ik}}$

$(\sigma_k^{new})^2 = \frac{\sum_{i=1}^N \gamma_{ik} (x_{i1} - \mu_k^{new})^2}{\sum_{i=1}^N \gamma_{ik}}$

3. ガンマ分布パラメータ： $\alpha_k^{new}$ と $\beta_k^{new}$ は、数値的に最適化する必要があります

$(\alpha_k^{new}, \beta_k^{new}) = \arg\max_{\alpha_k, \beta_k} \sum_{i=1}^N \gamma_{ik} \log P(x_{i2} | \alpha_k, \beta_k)$

4. 多項分布パラメータ：

$p_{kl}^{new} = \frac{\sum_{i=1}^N \gamma_{ik} x_{i3l}}{\sum_{i=1}^N \gamma_{ik} n_i}$

5. ベルヌーイ分布パラメータ：

$q_k^{new} = \frac{\sum_{i=1}^N \gamma_{ik} x_{i4}}{\sum_{i=1}^N \gamma_{ik}}$

これらのステップを、対数尤度が収束するまで、または指定した回数まで繰り返します。
この例では、4つの異なる分布を持つ変数を同時に扱う混合モデルにEMアルゴリズムを適用する方法を示しています。各分布のパラメータ更新式は、それぞれの分布の特性に基づいて導出されています。

ベイズアプローチ

混合確率分布クラスタリングモデルにおけるベイズアプローチでは、パラメータの事後分布全体を推定します。この方法では、パラメータを確率変数として扱い、データに基づいてその分布を更新します。ベイズの定理を用いると、パラメータθの事後分布は以下のように表現されます。

$p(\theta|X) \propto p(X|\theta)p(\theta)$

ここで、 $p(\theta|X)$ は事後分布、 $p(X|\theta)$ は尤度関数、 $p(\theta)$ は事前分布です。混合モデルの場合、尤度関数は以下のようにあらわされます。

$L(\theta, \pi | X) = \prod_{i=1}^N \sum_{k=1}^K \pi_k P(x_i | \theta_k)$

ここで

・ $N$ はデータ点の総数

・ $K$ はクラスタ数

・ $\pi_k$ は $k$ 番目のクラスターの混合比率

・ $\theta_k$ は $k$ 番目のクラスターのパラメータセット

・ $P(x_i|\theta_k)$ は $k$ 番目クラスターにおける $x_i$ の確率（または確率密度）

$P(x_i|\theta)$ は、各変数の確率分布の積として表現されます。

$P(x_i | \theta_k) = \prod_{j=1}^M P(x_{ij} | \theta_{kj})$

ここで、 $M$ は変数の数、 $x_{ij}$ は $i$ 番目のデータ点の $j$ 番目の変数、 $\theta_{kj}$ は対応するパラメータです。

　　
一つの混合モデルで、正規分布、ガンマ分布、多項分布が各変数で定義される場合の例を以下に示します。
例：顧客セグメンテーションこのモデルでは、以下の3つの変数を考慮する
1. 年齢（正規分布）
2. 年間支出額（ガンマ分布）
3. 好みの商品カテゴリ（多項分布）

各クラスタ $k$ に対して、尤度関数は以下のようにあらわされます。

$P(x_i | \theta_k) = P(x_{i1} | \mu_k, \sigma_k) \cdot P(x_{i2} | \alpha_k, \beta_k) \cdot P(x_{i3} | p_k)$

ここで、
　　
正規分布（年齢）

$P(x_{i1} | \mu_k, \sigma_k) = \frac{1}{\sigma_k\sqrt{2\pi}} \exp\left(-\frac{(x_{i1}-\mu_k)^2}{2\sigma_k^2}\right)$

$\mu_k$ は平均年齢、 $\sigma_k$ は年齢の標準偏差

　　
ガンマ分布（年間支出額）

$P(x_{i2} | \alpha_k, \beta_k) = \frac{\beta_k^{\alpha_k}}{\Gamma(\alpha_k)} x_{i2}^{\alpha_k-1} e^{-\beta_k x_{i2}}$

$\alpha_k$ は形状パラメータ、 $\beta_k$ は率パラメータ

　　
多項分布（好みの商品カテゴリ）

$P(x_{i3} | p_k) = \frac{n_i!}{x_{i31}!x_{i32}!\cdots x_{i3L}!} p_{k1}^{x_{i31}} p_{k2}^{x_{i32}} \cdots p_{kL}^{x_{i3L}}$

$n_i$ は総購入回数、 $x_{i3l}$ は $l$ 番目のカテゴリの購入回数、 $p_{kl}$ は $k$ 番目のクラスタにおける $l$ 番目のカテゴリが選ばれる確率

　　
したがって、全体の尤度関数は以下のようになる

$L(\theta, \pi | X) = \prod_{i=1}^N \sum_{k=1}^K \pi_k \left[P(x_{i1} | \mu_k, \sigma_k) \cdot P(x_{i2} | \alpha_k, \beta_k) \cdot P(x_{i3} | p_k)\right]$

　　
この事後分布は解析的に求めることが困難なため、マルコフ連鎖モンテカルロ法（MCMC）などのサンプリング手法を用いて近似します。MCMCは事後分布からのサンプリングを繰り返し行うことで、その分布の特性を推定する手法です。
MCMCサンプリングの一般的なプロセスは以下の通りです

1. パラメータの初期値 $\theta_0$ を設定する

2. 現在のパラメータ $\theta_t$ から、提案分布 $q(\theta'|\theta_t)$ を用いて新しいパラメータ $\theta'$ を生成する

3. 受理確率 $\alpha = \min(1, \frac{p(\theta'|X)q(\theta_t|\theta')}{p(\theta_t|X)q(\theta'|\theta_t)})$ を計算する

4. 確率 $\alpha$ で新しいパラメータを受理し、 $\theta_{t+1} = \theta'$ とする。確率 $1-\alpha$ で棄却し、 $\theta_{t+1} = \theta_t$ とする。

5. ステップ2-4を十分な回数繰り返す

十分な回数のサンプリングを行った後、得られたサンプルの集合が事後分布の近似となります。これらのサンプルを用いて、パラメータの期待値、分散、信頼区間などを計算することができます。　　
EMアルゴリズムとの比較では、ベイズアプローチはパラメータの不確実性をより詳細に扱える一方で、EMアルゴリズムは計算が高速で大規模データに適用しやすいという特徴があります。これは、EMアルゴリズムが高速な点推定が得意なためです。実務上は特徴量の数や扱うデータ量を鑑みると、EMアルゴリズムのほうが適切なのかもしれませんね。

モデルの評価と選択

混合確率分布モデルをどのように評価し、選択するかは、GMMの時と同様に、情報量基準を用いて評価し選択するのがいいのかなと感じています。AIC（赤池情報量基準）、BIC（ベイズ情報量基準）、WAIC（広く適用可能な情報量基準）などを用いて、モデルの複雑さとデータへの適合度のバランスを評価して選択することになるのかなと想定しています。
または、ベイズアプローチをとる場合は、生成された事後分布を使用して、事後分布からサンプリングしたパラメータを用いて趣味レーションデータを生成し、実際のデータと比較することによって、モデルの妥当性を評価できるという方法も考えられるかなと思います。
まあ後は、そもそも得られたクラスターが意味ある解釈をもつかどうかの判断ももちろん重要になってくると思います。というかこれが一番重要ですよね笑

オープンデータで実装してみましょう

今回はKaggleのオープンデータを使用してみましょう。カテゴリ変数や二値変数や連続値変数、連続値の中でもガンマ分布を規定できそうなデータがこれしか見つからなかったためです。Kaggleのアカウントを持っていない人は、Kaggleの登録が必要になってきますと思いますが、すみません。Kaggleの該当URLは以下になります。
kaggleデータURL

今回は、EMアルゴリズムによるパラメータ推定方法と、ベイズアプローチによるパラメータ推定の両方を実装し、比べてみると共に、決定論的アプローチであるK-meansとのクラスターを、PCAで次元削減した上で、クラスターの別れ方について比較してみたいと思います。今回はEMアルゴリズムによるパラメータ推定を試みたのですが、上手くいかな過ぎたので、ベイズアプローチによる推定のみを今回は扱うこととします。cmdstanoyには今回も結構苦しめられました...新しいノートパソコンに環境構築したらやはり思ったようにはいかず... ただ、各クラスターがどのような分布を持ち、どのような属性を持つのかを深堀った上で、比較するのが適切だと思いますが、そこまでする余裕は無いので、そこは省いた上で行う予定です。詳しく比較したい方は是非、比べてみてください。そして出来ればコメントにてどうだったか教えていただけると幸いです。

data {
  int<lower=1> N;  // データ点の数
  int<lower=1> D_normal;  // 正規分布に従う変数の数
  int<lower=1> D_gamma;  // ガンマ分布に従う変数の数
  int<lower=1> D_cat;  // カテゴリカル変数の次元
  int<lower=1> D_bin;  // 二値変数の数
  int<lower=1> D_count;  // カウントデータの数
  int<lower=1> K;  // クラスタ数
  matrix[N, D_normal] X_normal;  // 正規分布に従うデータ
  matrix[N, D_gamma] X_gamma;  // ガンマ分布に従うデータ
  matrix[N, D_cat] X_cat;  // カテゴリカルデータ（One-hotエンコーディング済み）
  array[N, D_bin] int<lower=0, upper=1> X_bin;  // 二値データ
  array[N, D_count] int<lower=0> X_count;  // カウントデータ
}

parameters {
  simplex[K] pi;  // 混合比率
  array[K] vector[D_normal] mu_normal;  // 正規分布の平均
  array[K] vector<lower=0>[D_normal] sigma_normal;  // 正規分布の標準偏差
  array[K] vector<lower=0>[D_gamma] alpha_gamma;  // ガンマ分布の形状パラメータ
  array[K] vector<lower=0>[D_gamma] beta_gamma;  // ガンマ分布の尺度パラメータ
  array[K] vector[D_cat] beta_cat;  // カテゴリカル変数の係数
  array[K] vector<lower=0, upper=1>[D_bin] p;  // 二値変数の確率
  array[K] vector[D_count] lambda;  // カウントデータのパラメータ
}

model {
  // 事前分布
  for (k in 1:K) {
    mu_normal[k] ~ normal(0, 5);
    sigma_normal[k] ~ cauchy(0, 5);
    alpha_gamma[k] ~ gamma(2, 2);
    beta_gamma[k] ~ gamma(2, 2);
    beta_cat[k] ~ normal(0, 5);
    p[k] ~ beta(1, 1);
    lambda[k] ~ normal(0, 5);
  }
  
  // 尤度
  vector[K] log_prob;
  for (n in 1:N) {
    for (k in 1:K) {
      log_prob[k] = log(pi[k]);
      log_prob[k] += normal_lpdf(X_normal[n] | mu_normal[k], sigma_normal[k]);
      log_prob[k] += gamma_lpdf(X_gamma[n] | alpha_gamma[k], beta_gamma[k]);
      log_prob[k] += X_cat[n] * beta_cat[k];  // カテゴリカルデータの処理を変更
      log_prob[k] += bernoulli_lpmf(X_bin[n] | p[k]);
      log_prob[k] += poisson_log_lpmf(X_count[n] | lambda[k]);
    }
    target += log_sum_exp(log_prob);
  }
}

generated quantities {
  array[N] simplex[K] responsibilities;
  for (n in 1:N) {
    vector[K] log_prob;
    for (k in 1:K) {
      log_prob[k] = log(pi[k]);
      log_prob[k] += normal_lpdf(X_normal[n] | mu_normal[k], sigma_normal[k]);
      log_prob[k] += gamma_lpdf(X_gamma[n] | alpha_gamma[k], beta_gamma[k]);
      log_prob[k] += X_cat[n] * beta_cat[k];  // カテゴリカルデータの処理を変更
      log_prob[k] += bernoulli_lpmf(X_bin[n] | p[k]);
      log_prob[k] += poisson_log_lpmf(X_count[n] | lambda[k]);
    }
    responsibilities[n] = softmax(log_prob);
  }
}

import pandas as pd
import numpy as np


from sklearn.preprocessing import StandardScaler, OneHotEncoder, PowerTransformer
from cmdstanpy import CmdStanModel
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from datetime import datetime
from tqdm import tqdm
import time
import codecs

def preprocess_data(data):
    # 年齢の計算（現在の年から生年を引く）
    current_year = datetime.now().year
    data['Age'] = current_year - data['Year_Birth']
    
    continuous_normal = ['Age']
    continuous_gamma = ['Income', 'MntWines', 'MntFruits', 'MntMeatProducts', 'MntFishProducts', 'MntSweetProducts', 'MntGoldProds']
    count_data = ['Kidhome', 'Teenhome', 'Recency', 'NumDealsPurchases', 'NumWebPurchases', 'NumCatalogPurchases', 'NumStorePurchases', 'NumWebVisitsMonth']
    categorical = ['Education', 'Marital_Status']
    binary = ['AcceptedCmp1', 'AcceptedCmp2', 'AcceptedCmp3', 'AcceptedCmp4', 'AcceptedCmp5', 'Complain', 'Response']

    # NaNの値を含む行を削除
    data = data.dropna(subset=continuous_normal + continuous_gamma + count_data + categorical + binary)

    # 正規分布に従うデータの処理
    X_normal = data[continuous_normal].values
    scaler_normal = StandardScaler()
    X_normal = scaler_normal.fit_transform(X_normal)

    # ガンマ分布に従うデータの処理
    X_gamma = data[continuous_gamma].values
    X_gamma = np.log1p(X_gamma)  # 対数変換
    scaler_gamma = StandardScaler()
    X_gamma = scaler_gamma.fit_transform(X_gamma)
    X_gamma = np.exp(X_gamma)  # 指数変換して戻す
    X_gamma = np.maximum(X_gamma, 1e-6)  # 小さな正の値で置き換え
    X_gamma = np.minimum(X_gamma, 1e6)   # 大きな値を制限

    # カウントデータの処理
    X_count = data[count_data].values
    X_count = np.log1p(X_count)  # 対数変換
    scaler_count = StandardScaler()
    X_count = scaler_count.fit_transform(X_count)
    X_count = np.maximum(X_count, 0)  # 負の値を0に置き換え
    X_count = data[count_data].values.astype(int)  # 整数型に変換

    # カテゴリカル変数のOne-hotエンコーディング
    encoder = OneHotEncoder(sparse_output=False, handle_unknown='ignore')
    X_categorical = encoder.fit_transform(data[categorical])
    
    # カテゴリカルデータの形状を確認
    print("X_categorical shape:", X_categorical.shape)
    print("X_categorical unique values:", np.unique(X_categorical))

    # 二値変数の準備
    X_binary = data[binary].values

    print("X_normal statistics after preprocessing:")
    print(pd.DataFrame(X_normal, columns=continuous_normal).describe())
    print("\nX_gamma statistics after preprocessing:")
    print(pd.DataFrame(X_gamma, columns=continuous_gamma).describe())

    return X_normal, X_gamma, X_count, X_categorical, X_binary

# データの読み込みと前処理
data = pd.read_csv('marketing_campaign.csv', sep='\t')
X_normal, X_gamma, X_categorical, X_binary, X_count = preprocess_data(data)

# Stanモデルのコンパイルと実行
model = CmdStanModel(stan_file='mixed_model.stan')

# クラスター数の設定
K = 3  # クラスター数を変更する場合はここを調整

# Stanモデルへの入力データの準備
stan_data = {
    'N': X_normal.shape[0],
    'D_normal': X_normal.shape[1],
    'D_gamma': X_gamma.shape[1],
    'D_cat': X_categorical.shape[1],
    'D_bin': X_binary.shape[1],
    'D_count': X_count.shape[1],
    'K': K,
    'X_normal': X_normal,
    'X_gamma': X_gamma,
    'X_cat': X_categorical,  # One-hotエンコーディング済みのデータをそのまま渡す
    'X_bin': X_binary.astype(int),
    'X_count': X_count.astype(int)
}

# モデルのサンプリング
# モデルのサンプリング
fit = model.sample(
    data=stan_data,
    iter_warmup=2000,
    iter_sampling=2000,
    chains=4,
    show_console=True,
    adapt_delta=0.95,
    max_treedepth=15
)

# 結果の抽出
responsibilities = fit.stan_variable('responsibilities')

# クラスタリング結果の可視化
def plot_clusters(X, responsibilities, title):
    pca = PCA(n_components=2)
    X_pca = pca.fit_transform(X)
    
    plt.figure(figsize=(10, 8))
    scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=responsibilities.mean(axis=0).argmax(axis=1), cmap='viridis', alpha=0.5)
    plt.colorbar(scatter)
    plt.title(title)
    plt.xlabel('First Principal Component')
    plt.ylabel('Second Principal Component')
    plt.show()

# すべての特徴量を結合
X_all = np.hstack([X_normal, X_gamma, X_categorical, X_binary, X_count])

# クラスタリング結果の可視化
plot_clusters(X_all, responsibilities, f'Mixed Clustering (K={K})')

# クラスターごとの特徴を表示
for k in range(K):
    cluster_probs = responsibilities.mean(axis=0)[:, k]
    top_indices = np.argsort(cluster_probs)[-10:]  # 上位10個のデータポイント
    print(f"\nCluster {k+1} 特徴:")
    for idx in top_indices:
        print(f"データポイント {idx}: クラスター所属確率 = {cluster_probs[idx]:.4f}")
        print(data.iloc[idx])
        print("---")

このコードですが、実行に245時間かかりました...EMアルゴリズムが変な感じにならなければ、もっと速い速度で計算が終わるのですが、stanを使うとなると相当時間がかかりますね...
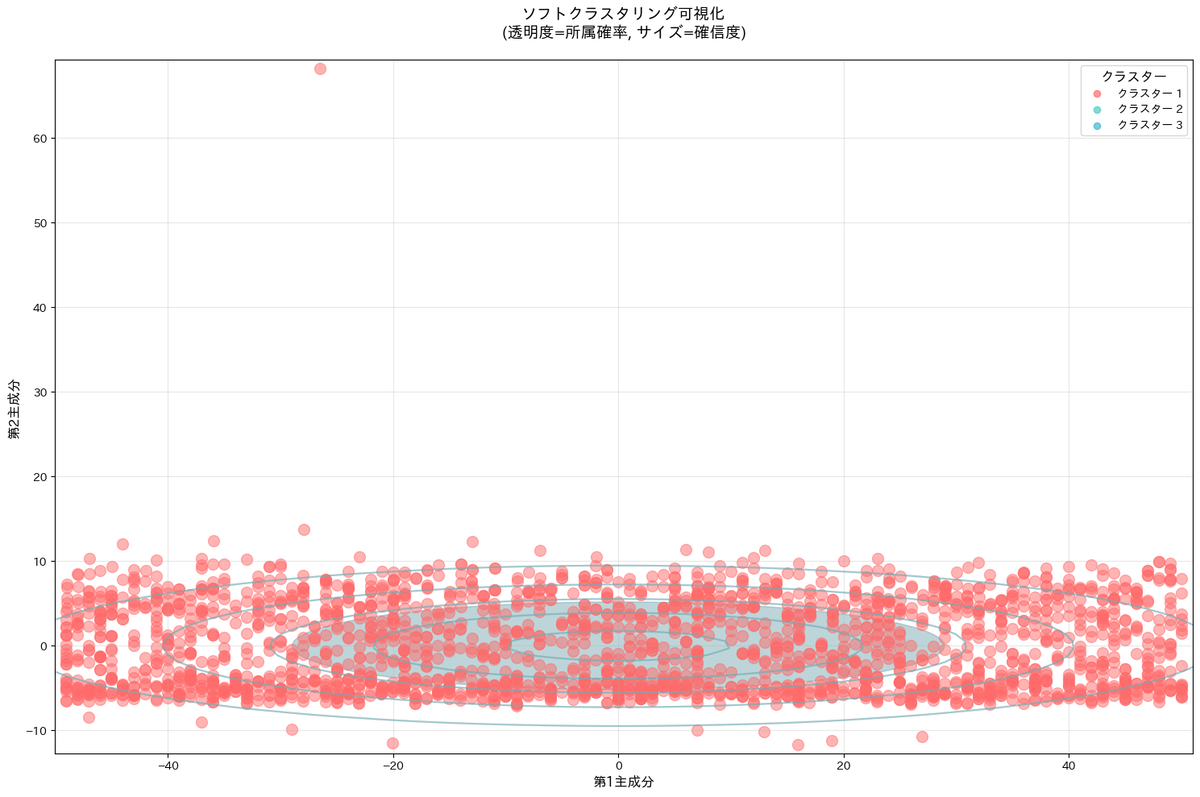これが結果です。実行に時間がかかりすぎたので、前処理部分やstanファイルの中身を調整すれば、まともな結果になるのかとも思いつつ、混合確率モデル的なモデルが実務などで使用されてこなかったことがなんとなくわかりましたね。いいモデルだとは思いつつ、誰も使用してこなかったことにはいろいろ理由があったんだなということが良く分かった結果でした。

最後に

実行時間にとても時間がかかり、個人的に葉ずっとPCのCPU使用率をずっと占領され続けたので、結果に期待していたのですが、理想的なモデルが理想的に動くとは限らないということを思い知らされました。ただ、混合ガウスの正規分布の規定を外し自由にという発想は、いいなと思うので計算量を考慮しつつ、EMアルゴリズム的な方法で局所解に陥らず、パラメータ推定が可能な方法をこれからも探っては行きたいなと思いました。とりあえずstanは調整すれば理想的な結果が得られるような気もするが、計算量が多すぎてPoCを回せず実務に耐えられないということがわかりました。
また別の方向性ですが、混合ガウスのようにある程度強めの仮定を置いて自由度を制限するというのも手かもしれませんね。最後までお読みいただきありがとうございました。

tomtom58’s blog

混合確率分布クラスタリングモデルの理論と実装