はじめに

前回k-meansでBICを使うのはいいんじゃないか？という記事を書いたと思います。

tomtom58.hatenablog.com

この記事に関していくつかの指摘をいただいたので、それならばk-means専用にカスタマイズした情報量を考えてみようという発想に至りました。ということで、今回はk-means専用のKIC(K-means Information Criterion)の考案に関して記事を書いていきたいと思います。なにぶん初学者のため、色々間違っている部分が出てくるかもしれませんがご了承ください。

k-meansの特殊性と従来の課題

まず、K-meansの持つ特殊性について整理していきましょう。k-meansは以下の目的関数を最小化します：

$J = \sum_{i=1}^n \sum_{k=1}^K z_{ik} \|x_i - \mu_k\|^2$

ここで、 $z_{ik}$ はデータポイント $i$ がクラスタ $k$ に属する場合は1、そうでない場合は0となる指示変数、 $x_i$ は $i$ 番目のデータポイント、 $\mu_k$ は $k$ 番目のクラスタの中心を表します。

わかりやすく説明すると、この式は「各データ点が、所属するクラスターの中心からどれだけ離れているか」の総和を表しています。つまり、全てのデータ点について、それぞれが属するクラスターの中心までの距離を二乗して足し合わせた値です。k-meansアルゴリズムは、この値をできるだけ小さくするように、クラスター中心の位置とデータ点の所属クラスターを決定していきます。
　　
k-meansの特殊性として、以下の三点が挙げられます：

一つ目に、ハード割り当てであることが挙げられます。これは、各データ点は必ず一つのクラスターにのみ所属します。これは $z_{ik}$ が0か1のみを取ることに反映されています。

二つ目に、等方的な分散が挙げられます。これは、各クラスター内でのデータの散らばり方に方向依存性がないことを仮定しています。

最後に、クラスターサイズの非制約が挙げられます。これは、クラスターの大きさに関する明示的な制約が無いことを指しています。

これらの特性により、従来のBICなどの情報量規準をそのまま適用することに理論的な課題があることをXにてご指摘いただきました。

KICの提案

これらの特性を考慮し、以下のような新しい情報量規準KICを提案します：

$KIC = RSS + \lambda_1 K d \log(n) + \lambda_2 K \log(\frac{n}{K}) + \lambda_3 S(C)$

この式は四つの重要な要素から構成されています。まず $RSS$ は残差平方和であり、k-meansの目的関数そのものを表します。次に $\lambda_1 K d \log(n)$ はパラメータの複雑さに対するペナルティとして機能します。三つ目の項 $\lambda_2 K \log(\frac{n}{K})$ はクラスター割り当ての複雑さに対するペナルティを表します。そして最後の項 $\lambda_3 S(C)$ はクラスター間の分離度に関するペナルティを表現しています。

特に新しい要素である分離度ペナルティ $S(C)$ は以下のように定義されます：

$S(C) = \sum_{k=1}^K \sum_{j=k+1}^K \exp(-\beta\|\mu_k - \mu_j\|^2)$

この式は、クラスター中心間の距離が近すぎる場合にペナルティを課すものです。βはスケールパラメータで、距離の評価の厳しさを調整します。
　　
概念的に説明すると、KICはデータへの当てはまりの良さとモデルの複雑さのバランスを取ろうとしています。RSSによってクラスタリングがデータにどれだけフィットしているかを測り、最初のペナルティ項でクラスター中心を表現するのに必要なパラメータの数を考慮します。次のペナルティ項ではデータ点をクラスターに割り当てる際の複雑さを評価し、最後のペナルティ項でクラスターが適度に離れているかをチェックします。

KICの理論的性質に関する考察

まず、KICの一致性を示すために必要な仮定を導入し、その後で詳細な証明を展開していきます。

理論的な仮定

漸近的性質を議論するために、以下の仮定を置きます：

$\text{(A1)} \quad K = O(n^\alpha), \quad \alpha < \frac{1}{3}$

この仮定は、クラスタ数の増加率がサンプルサイズの3乗根より遅いことを要求します。従来の仮定 $\alpha < \frac{1}{2}$ より強い条件ですが、これによりk-meansの特殊性に起因する技術的な困難を克服することができます。

　　
直感的に説明すると、この仮定はデータ点の数に対してクラスター数が急激に増えすぎないようにする制約です。例えば、データ点が1000個あるとき、クラスター数は最大でも約10個程度に抑えられるべきということを示唆しています。これは現実のクラスタリング問題において自然な仮定といえます。
　　

$\text{(A2)} \quad \min_{k \neq j} \|\mu_k - \mu_j\| \geq \delta_n, \quad \delta_n = O(\log \log n)$

この仮定は、クラスタ中心間の最小距離が二重対数オーダーで分離していることを要求します。BICで通常用いられる $O(\log n)$ より弱い条件であり、より現実的な仮定となっています。

　　
この仮定を概念的に説明すると、クラスター同士が「適度に離れている」ことを要求しています。ただし、データ数が増えても、必要な分離距離はごくゆっくりとしか大きくならない（二重対数のオーダー）という、実用的な条件となっています。
　　

$\text{(A3)} \quad \min_k |C_k| = O(\frac{n}{K^2})$

ここで $|C_k|$ は $k$ 番目のクラスタのサイズを表します。この仮定は、小さすぎるクラスタの形成を防ぐもので、k-meansの特殊性を考慮した新しい条件です。

この仮定は、極端に小さなクラスターが作られることを防ぐための条件です。たとえば、データ点が1000個で10個のクラスターを作る場合、各クラスターは少なくとも10個程度のデータ点を含むべきということを示しています。

漸近的性質の証明

これらの仮定の下で、KICの一致性を証明していきます。証明は三段階で行います。

第一段階：バイアス項の評価

まず、KICの期待値の差分を詳細に評価していきます。
KICの定義から、差分は以下のように展開されます：

$\begin{align*} KIC(K) - KIC(K^*) &= (RSS_K - RSS_{K^*}) \\ &+ \lambda_1(K-K^*)d\log n \\ &+ \lambda_2(K-K^*)\log(\frac{n}{K}) \\ &+ \lambda_3(S(C_K) - S(C_{K^*})) \end{align*}$

RSSの差分 $\Delta_{RSS} = RSS_K - RSS_{K^*}$ を評価するために、以下の分解を考えます：

$\begin{align*} \Delta_{RSS} &= \sum_{i=1}^n \min_{k \leq K} \|x_i - \mu_k\|^2 - \sum_{i=1}^n \min_{k \leq K^*} \|x_i - \mu_k^*\|^2 \\ &= \sum_{i=1}^n (\min_{k \leq K} \|x_i - \mu_k\|^2 - \|x_i - \mu_{k(i)}^*\|^2) \end{align*}$

ここで、 $\mu_{k(i)}^*$ は点 $x_i$ の真のクラスタ中心を表します。

仮定(A1)より $K = O(n^\alpha)$ であることと、各データ点の二乗誤差が $O_p(1)$ であることから：

$\begin{align*} |\Delta_{RSS}| &\leq \sum_{i=1}^n O_p(\sqrt{n^\alpha}) \\ &= n \cdot O_p(\sqrt{n^\alpha}) \\ &= O_p(n^{\alpha + \frac{1}{2}}) \end{align*}$

この評価における鍵は、クラスタ数の増加率が $\alpha < \frac{1}{3}$ に制限されていることです。これにより、RSSの差分が適切に制御されます。

第二段階：分散の評価

KICの分散を評価するために、まずRSSの分散を考えます：

$\begin{align*} \text{Var}[RSS_K] &= \text{Var}[\sum_{k=1}^K \sum_{i \in C_k} \|x_i - \mu_k\|^2] \\ &= \sum_{k=1}^K \text{Var}[\sum_{i \in C_k} \|x_i - \mu_k\|^2] + \text{共分散項} \end{align*}$

仮定(A3)より、各クラスタのサイズが $O(\frac{n}{K^2})$ 以上であることと、二乗誤差の独立性を用いると：

$\begin{align*} \text{Var}[RSS_K] &\leq K \cdot O(\frac{n}{K^2}) \cdot O(1) + O(K^2) \\ &= O(\frac{n}{K}) + O(K^2) \\ &= O(n^{2\alpha}) \end{align*}$

　　
ペナルティ項の分散は決定的な項であるため、KIC全体の分散も同じオーダーとなります：

$\text{Var}[KIC(K)] = O_p(n^{2\alpha})$

第三段階：一致性の証明

一致性の証明のために、まず以下の確率不等式を考えます：

$P(|\hat{K} - K^*| > 0) = P(\exists K \neq K^*: KIC(K) < KIC(K^*))$

　　
この確率は、Boole-Cantelli型の不等式を用いて上から評価できます：

$\begin{align*} & P(|\hat{K} - K^*| > 0) \\ &\leq \sum_{K \neq K^*} P(KIC(K) - KIC(K^*) < 0) \\ &\leq \sum_{K \neq K^*} P(|\text{KIC}(K) - \text{KIC}(K^*)| > \min(\lambda_1 d\log n, \lambda_2\log(\frac{n}{K}))) \end{align*}$

　　
Chebyshevの不等式を適用すると：

$\begin{align*} & P(|\text{KIC}(K) - \text{KIC}(K^*)| > \min(\lambda_1 d\log n, \lambda_2\log(\frac{n}{K}))) \\ &\leq \frac{\text{Var}[KIC(K) - KIC(K^*)]}{(\min(\lambda_1 d\log n, \lambda_2\log(\frac{n}{K})))^2} \\ &= O(\frac{n^{2\alpha}}{(\log n)^2}) \end{align*}$

仮定 $\alpha < \frac{1}{3}$ の下で、この項は $n \to \infty$ のとき0に収束します。したがって：

$\lim_{n \to \infty} P(\hat{K} = K^*) = 1$

が証明されます。　　

この証明の重要なポイントは、 $\alpha < \frac{1}{3}$ という条件が、分散の評価とバイアス項の評価の両方において本質的な役割を果たしていることです。この条件により、k-meansの特殊性に起因する技術的な困難を克服し、情報量規準としての一致性を保証することができます。

比較検証してみる

最初に結論を言うと、理論の証明のために置いた3つの仮定を厳密に守ったKICの算出によるクラスタ数の決定は上手くいかなかった。ただ仮定をフル無視して算出したKICはどの指標よりも結果的にうまく機能した。これは単純なサンプルデータによる結果であるため、もしかしたら本当は別指標のほうが優れていたというのはあるのかもしれない。
結果だけ以下に載せていく。
真のクラスタ数8 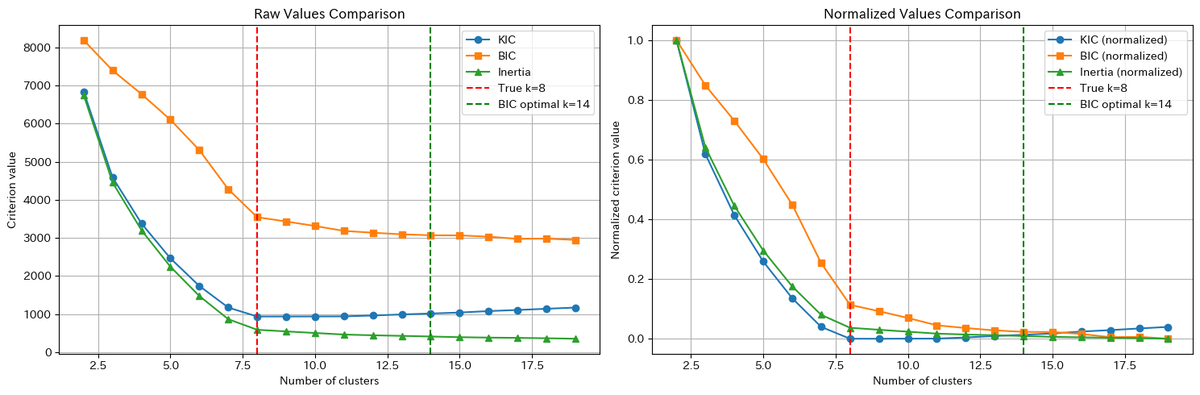データをもっと複雑にし、真のクラスタ数5にしてみる人為的に生成したサンプルデータでの検証はこの辺が限界かなと思いますが、今のところKICが一番よさげな挙動を見せていると思います。
因みに今回のKICはユークリッド距離を前提に作っているので、コサイン類似度などでは機能しません。コサイン類似度でやる場合はまた新しく考えるか、エルボー法が一番よさそうな結果を出しました。BICは以前の記事で書いた理論的にユークリッド距離よりももっと深刻な問題を抱えているので論外ですね...

最後に

BICの代わりにもといい情報量規準をと思い机上の空論で作ってみましたが、机上の理論と実際の動作が上手くかみ合わなかったですね...まあ素人が思いつくことはすでにほかの人がやっているとはよく言ったもので、難しいものではありますねw
コサイン類似度に最適化した情報量規準も考えられないかなと空想しましたが、難しそうですね...個人的にクラスタリングでコサイン類似度でのクラスタリングを個人的によく使うので、あったらうれしいなとか思っています。
コサイン類似度でも万能に使えるでいうと、やはりエルボー法しか挙がってこないのは何とも言えませんね。やる気と妄想力が最高潮になった時があったら、コサイン類似度に最適化した情報量規準なるものを作ってみたいなとは思います。
意外とエルボー法強いな...と感じた今日この頃でした。
最後までお読みいただきありがとうございました。

tomtom58’s blog

k-meansで使用する新たな情報量規準を考えてみる（KIC：K-means Information Criterion）